Lernauftrag 27: Auswirkungen unsymmetrischer Belastung beschreiben
Hier findest du die Aufgaben ohne Lösungen.
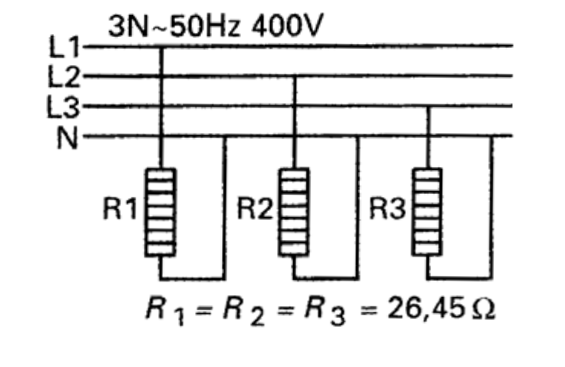
Drehstromverbraucher (z.B. Drehstrommotoren, Drehstromspeicherofen) belasten das Netz im Allgemeinen symmetrisch, d.h. sie rufen in jedem Außenleiter die gleichen Ströme hervor. (In jedem Strang ist ein Lastwiderstand gleicher Größe)
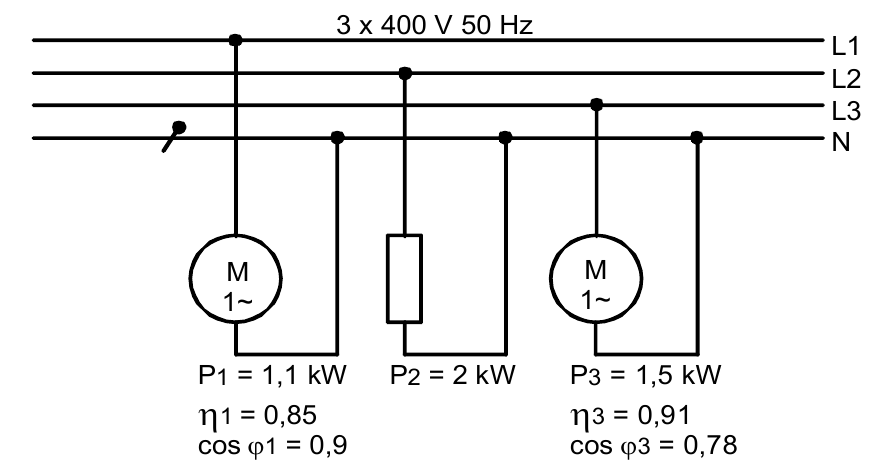
Unsymmetrische Belastung kann beispielsweise durch einphasige Verbraucher hervorgerufen werden, die zwischen einem Außenleiter und dem Neutralleiter geschaltet sind. Sind die Belastungswiderstände, die an die Außenleiter angeschlossen unterschiedlich, so fließen auch unterschiedliche Ströme.
Aufgabe 1
Ermittle ob die Darstellungen Schaltung in Y oder \(\Delta\) Form darstellen.
Y-Schaltung
Aufgabe 2
Berechne für die symmetrische Belastung (oberes Bild):
1) die Ströme durch die einzelnen Verbraucher
2) den Strom in der Zuleitung
3) die Leistungsaufnahme jedes Heizwiderstandes
4) Gesamtleistung des Speicherofens.
geg: \(R=26,45\ \Omega, U=400\ V\)
ges: \(I_{Str}\)
Lös: \(U_{Str}=R\cdot I_{Str}\Leftrightarrow I_{Str}=\frac{U_{Str}}{R}=\frac{U}{\sqrt{3}\cdot R}=\frac{400\ V}{\sqrt{3}\cdot26,45\ \Omega}=8,73\ A\)
ges: \(I\)
Lös: Y-Schaltung \(\Rightarrow I=I_{Str}=8,73\ A\)
ges: \(S_{Str}\)
Lös: \(S_{Str}=U_{Str}\cdot I_{Str}=\frac{U}{\sqrt{3}}\cdot I_{Str}=\frac{400\ V\cdot 8,73\ A}{\sqrt{3}}=2016\ W=2\ kW\)
ges: \(S_{ges}\)
Lös: \(S_{ges}=3\cdot S_{Str}=3\cdot 2\ kW=6\ kW\)
Aufgabe 3
Berechne für die unsymmetrische Belastung (unteres Bild):
1) die Ströme durch die einzelnen Verbraucher
2) den Strom in der Zuleitung
3) die Leistungsaufnahme jedes Heizwiderstandes
4) Gesamtleistung der Verbraucher.
geg:
\(U=400\ V\)
\(P_1=1,1\ kW, \eta_1=0,85, \cos\varphi_1=0,9\)
\(P_2=2\ kW\)
\(P_3=1,5\ kW, \eta_3=0,91, \cos\varphi_3=0,78\)
ges: \(I_{Str,1}, I_{Str,2}, I_{Str,3}\)
Lös:
Für Verbraucher 1 und 3 müssen wir den Wirkungsgrad \(\eta\) berücksichtigen. Erinnern wir uns, daß der Wirkungsgrad \(\eta=\frac{P_{ab}}{P_{zu}}\) ist. Die am Verbraucher angegebene Leistung ist die Leistung, welcher er abgibt (\(P_{ab}\)). Damit wir jedoch den Strom, welchen der Verbraucher aufnimmt, berechnen können benötigen wir jeweils (\(P_{zu}\)).
Korrigieren wir also zuerst die Leistungen \(P_1\) und \(P_3\) um den jeweiligen Wirkungsgrad:
\(\eta=\frac{P_{ab}}{P_{zu}}\Leftrightarrow P_{zu}=\frac{P_{ab}}{\eta}\)
\(P'_1=\frac{P_1}{\eta_1}=\frac{1,1\ kW}{0,85}=1294\ W\)
\(P'_3=\frac{P_3}{\eta_3}=\frac{1,5\ kW}{0,91}=1648\ W\)
Der Strom durch einen Verbraucher entspricht dem Strangstrom und berechnet sich zu
\(P=\cos\varphi\cdot U_{Str}\cdot I_{Str}\Leftrightarrow I_{Str}=\frac{P}{U_{Str}\cdot\cos\varphi}=\frac{\sqrt{3}\cdot P}{U\cdot\cos\varphi}\)
\(I_{Str,1}=\frac{\sqrt{3}\cdot P'_1}{U\cdot\cos\varphi_1}=\frac{\sqrt{3}\cdot 1294\ W}{400\ V\cdot 0,9}=6,23\ A\)
\(I_{Str,1}=\frac{\sqrt{3}\cdot P'_1}{U\cdot\cos\varphi_2}=\frac{\sqrt{3}\cdot 1294\ W}{400\ V\cdot 1}=8,66\ A\)
\(I_{Str,3}=\frac{\sqrt{3}\cdot P'_3}{U\cdot\cos\varphi_3}=\frac{\sqrt{3}\cdot 1648\ W}{400\ V\cdot0,78}=9,15\ A\)
ges: \(I\)
Lös: \(I=I_{Str,1}+I_{Str,2}+I_{Str,3}=6,23\ A+8,66\ A+9,15\ A=24,04\ A\)
ges: \(S_{Str,1}, S_{Str,2}, S_{Str,3}\)
Lös:
\(S_{Str}=U_{Str}\cdot I_{Str}=\frac{U}{\sqrt{3}}\cdot I_{Str}\)
\(S_{Str,1}=\frac{U\cdot I_{Str,1}}{\sqrt{3}}=\frac{400\ V\cdot6,23\ A}{\sqrt{3}}=1438\ VA=1,438\ kVA\)
\(S_{Str,2}=\frac{U\cdot I_{Str,2}}{\sqrt{3}}=\frac{400\ V\cdot8,66\ A}{\sqrt{3}}=1999,94\ VA=2\ kVA\)
\(S_{Str,3}=\frac{U\cdot I_{Str,3}}{\sqrt{3}}=\frac{400\ V\cdot9,15\ A}{\sqrt{3}}=2113\ VA=2,113\ kVA\)
ges: \(S_{ges}\)
Lös: \(S_{ges}=S_{Str,1}+S_{Str,2}+S_{Str,3}=(1,438+2+2,113)\ kVA=5,55\ kVA\)
Aufgabe 4
Beschreibe welche Auswirkung unsymmetrische Belastung auf der Netzsystem hat.
Bei unsymmetrischer Belastung fließt Strom durch den Neutralleiter zurück. Das bedeutet Verluste, da nicht der gesamte zufließende Strom in Leistung umgesetzt wird.
Wäre das System Neutralleiterbefreit wäre es gleichbedeutend mit einer Sternpunktverschiebung und als Folge dessen verändern die Strangspannungen ihren Betrag und ihre Richtung, was zu Über- bzw. Unterspannungen an den Verbrauchern führt.
Als logische Ableitung gilt: Misst man an den Wechselstromverbrauchern in einem Drehstromsystem unterschiedliche Spannungen, so ist der Neutralleiter entweder nicht angeschlossen oder unterbrochen.