Lernauftrag 18: Wirkung von induktiven Blindwiderständen kompensieren
Hier findest du Aufgaben ohne Lösungen.
Gemäß § 16 Abs. 2 NAV hat die Anschlussnutzung mit einem Verschiebungsfaktor (\(\cos\varphi\)) zwischen 0,9 kapazitiv und 0,9 induktiv zu erfolgen. Andernfalls kann der Netzbetreiber den Einbau ausreichender Kompensationseinrichtungen verlangen.
Einrichtungen zur Blindleistungskompensation werden entweder zusammen mit den Verbrauchsgeräten zu-bzw. abgeschaltet oder über Regeleinrichtungen betrieben.
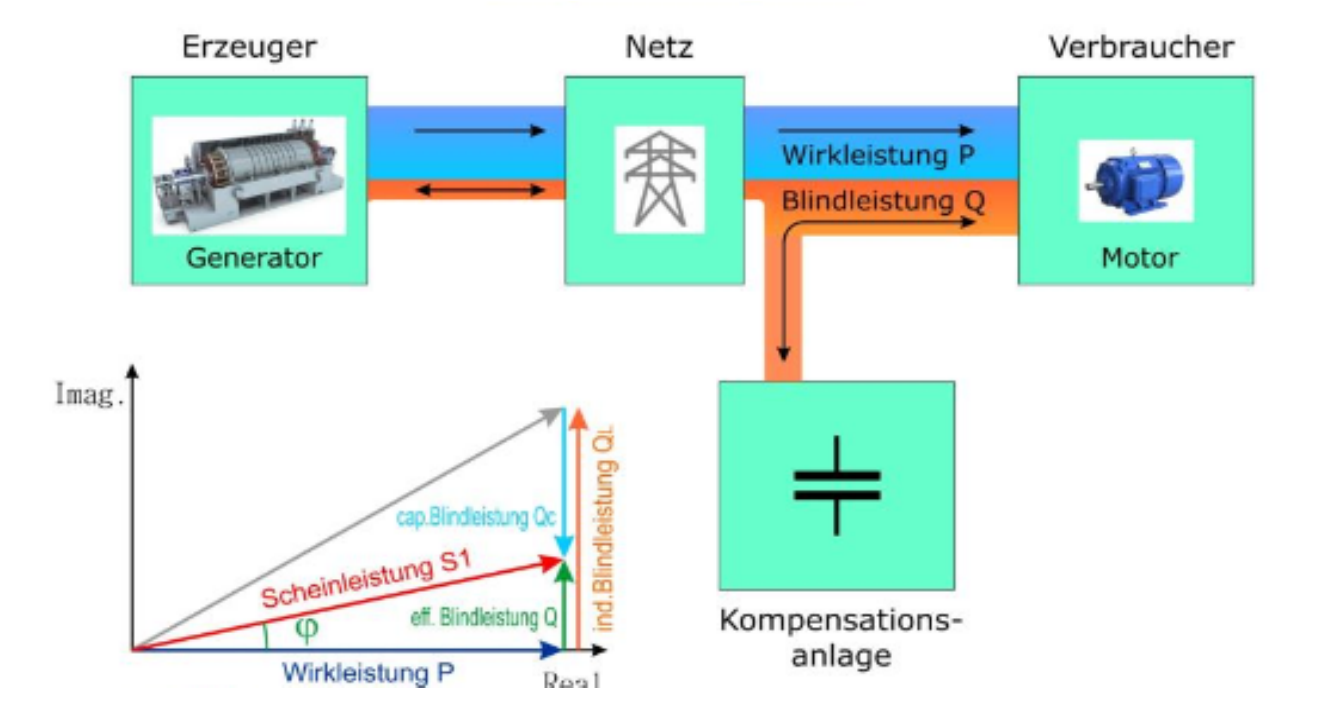
| ausgewählte Betriebsmittel (nicht kompensiert) | Leistungsfaktor \(\cos\varphi\) |
|---|---|
| leerlaufende Transformatoren | 0,1 - 0,4 |
| leerlaufende Wechselstrommotoren | 0,3 - 0,6 |
| Leuchtstofflampen (mit induktivem Vorschaltgerät) | 0,5 |
| belastete Wechselstrommotoren | 0,6 - 0,8 |
| belastete Drehstrommotoren | 0,7 - 0,8 |
| belastete Transformatoren | 0,85 - 0,99 |
| Glühlampen, Elektrowärmegeräte | 1 |
Ein "guter" Leistungsfaktor bringt als wirtschaftlichen Nutzen:
- die Verringerung des Energieaufwandes bei gleicher Wirkleistung,
- die Reduzierung der Leitungsbelastung (Stromwärme),
- die Verringerung der Verluste (Spannungsabfälle) und
- Einsparung von Werkstoffen (Verringerung der Querschnitte).
Auftrag
Die abgebildete Leuchtstofflampe mit den Nennbemessungswerten \(230\ V; 36\ VA\) benötigt zur Zündung und zum dauerhaften Betrieb ein Vorschaltgerät. Die Brennspannung der Leuchtstofflampe beträgt \(80\ V\).
Du erhältst den Auftrag, durch das Hinzuschalten eines entsprechend dimensionierten Kondensators die Wirkung der induktiven Blindleistung des Vorschaltgerätes zu kompensieren.
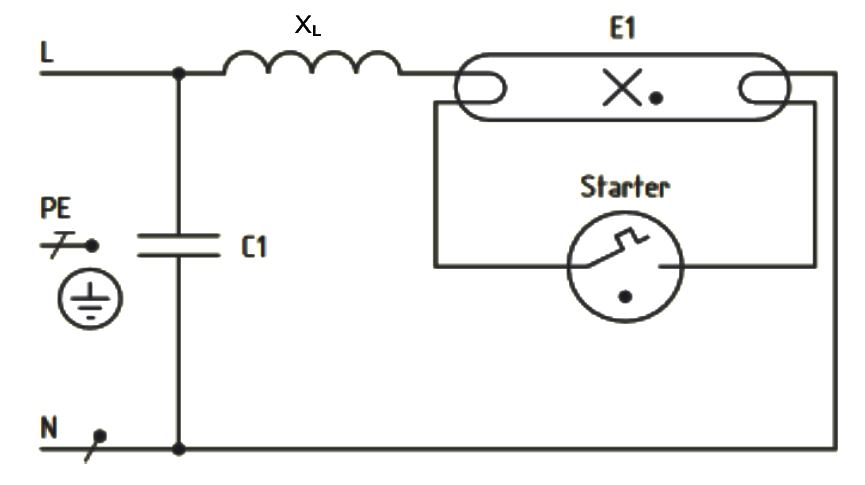
Löse die folgenden Aufgaben, welche eine Anleitung darstellen, mit welcher die Kapazität \(C_1\) für die vollständige Kompensation der induktiven Blindleistung berechnet werden kann.
Aufgabe 1
Zeichne dir schematisch drei induktive Dreiecke (Spannungs-, Widerstands- und Leistungsdreieck) und schreibe an die Seite die elektrischen Größen. Vermerke an den Dreiecken für welche Größen du aus der Aufgabenstellung bereits Werte kennst.
Dreiecke zeichnen und Größen vermerken siehe Lösungen zu Lernauftrag 14. Hier werden folgende Größen als bekannt vermerkt:
\(U=230\ V\)
\(U_W=80\ V\)
\(S=36\ VA\)
\(f=50\ Hz\)
Aufgabe 2
Betrachte deine Dreiecke und schau, welche Größen du leicht ermitteln kannst und berechne diese.
Hinweis: \(\varphi\) ist in allen drei Dreiecken gleich groß.
Phasenwinkel (\(U, U_W\) gegeben):
\(\cos\varphi=\frac{U_W}{U}\Leftrightarrow \varphi=\cos^{-1}\left(\frac{80\ V}{230\ V}\right)=69,7°\)
Strom (\(S, U\) gegeben):
\(S=U\cdot I\Leftrightarrow I=\frac{S}{U}=\frac{36\ VA}{230\ V}=156,5\ mA\)
Spannungen (\(U, U_W\) gegeben):
\(U_L=\sqrt{U^2-U_W^2}=215,6\ V\)
Leistungen (\(S\) gegeben):
\(P=S\cdot\cos\varphi=12,5\ W\)
\(Q_L=\sqrt{S^2-P^2}=33,8\ var\)
Widerstände:
\(U=Z\cdot I\Leftrightarrow Z=\frac{U}{I}=\frac{230\ V}{156,5\ mA}=1,47\ k\Omega\)
\(R=Z\cdot\cos\varphi=511\ \Omega\)
\(X_L=\sqrt{Z^2-R^2}=1,378\ k\Omega\)
Aufgabe 3
Sofern nicht schon in Aufgabe 2 erledigt, berechne die vom Verbraucher aufgenommene Blindleistung \(Q_L\).
Siehe Aufgabe 2 \(\rightarrow Q_L=33,8\ var\)
Aufgabe 4
Um die Blindleistung \(Q_L\) zu kompensieren, muß der Kondensator eine kapazitive Blindleistung der gleichen Höhe haben. Es muß also gelten:
\(Q_L=Q_C\)
also
\(Q_C=Q_L=33,8\ var\)
Berechne mit der Überlegung die Kapazität des Kondensators \(C_1\) mit Hilfe der Formel:
Motivieren wir zuerst woher eigentlich die Formel kommt.
Für den kapazitiven Blindwiderstand gilt:
\(X_C=\frac{1}{\omega\cdot C}\)
Ferner gilt für die kapazitive Blindleistung \(Q_C\) in dem parallen Pfad:
\(Q_C=U_C\cdot I=U\cdot I\)
denn in dem Pfad gibt es nur den Kondensator und somit fällt die gesamte Spannung darüber ab.
Ersetzen wir den Strom \(I\) durch Spannung und kapazitiven Blindwiderstand \(X_C\), also \(U=X_C\cdot I\Leftrightarrow I=\frac{U}{X_C}\), so erhalten wir
\(Q_C=\frac{U^2}{X_C}\)
stellen wir das um auf \(X_C\) so erhalten wir
\(X_C=\frac{U^2}{Q_C}\)
Das setzen wir in die Formel für den kapazitiven Blindwiderstand ein und erhalten
\(\frac{U^2}{Q_C}=\frac{1}{\omega\cdot C}\)
und stellen diese Formel auf \(C\) um und erhalten
\(C=\frac{Q_C}{\omega\cdot U^2}\)
geg: \(Q_C=33,8\ var, U=230\ V, f=50\ Hz\)
ges: \(C_1\)
Lös: \(C_1=\frac{Q_C}{\omega\cdot U^2}=\frac{Q_C}{2\cdot\pi\cdot f\cdot U^2}=\frac{33,8\ var}{2\cdot\pi\cdot 50\ Hz\cdot(230\ V)^2}=2\cdot10^{-6}\ F=2\ \mu F\)
Antw: Die notwendige Kapazität beträgt \(2\ \mu F\).
Aufgabe 5
Lies dir im Fachbuch Abschnitt 7.10 Kompensation bis einschließlich 7.10.2 durch. Achte insbesondere auf Reihen- und Parallelkompensation.
Zusatzaufgabe 6
Alternativ zu den verwendeten Formeln kann mit Hilfe der ermittelten Widerstandswerte \(Z, X_L\) und \(R\) die Parallelkompensation vorgenommen werden.
Nutze S. 46 des Tabellenbuchs und finde eine Formel wie bei bekanntem Scheinwiderstand \(Z\) ein Reihenwiderstand \(R_r\) in einen Parallelwiderstand \(R_p\) gewandelt werden kann. Das gleiche Prinzip läßt sich auch auf Blindwiderstände anwenden, sprich \(X_r\) wird ersetzt durch \(X_p\).
Überführe auf diese Weise die Reihenschaltung von \(X_{L}\) und \(R\) in eine Parallelschaltung von \(R_p\) und \(X_{L_p}\).
Der parallel zu schaltende Kompensationskondensator \(X_C\) muss den gleichen Blindwiderstandswert wie die Drossel (Spule) \(X_{L_p}\) haben.
\(X_C=X_{L_p}\)
Berechne \(X_C\) und daraus erneut die Kapazität \(C\). Vergleiche das Ergebnis mit Aufgabe 4.
Die Formel lautet:
\(R_p=\frac{Z_r^2}{R_r}\)
Da erreichen wollen, daß die Reihenschaltung in eine äquivalente Parallelschaltung übergeht muss gelten \(Z=Z_r=Z_p\), also wird die Formel vereinfacht zu
\(R_p=\frac{Z^2}{R_r}\) bzw. \(X_{L_p}=\frac{Z^2}{X_L}\)
setzen wir ein:
\(R_p=\frac{(1,47\ k\Omega)^2}{0,511\ k\Omega}=4,229\ k\Omega\)
\(X_{L_p}=\frac{(1,47\ k\Omega)^2}{1,378\ k\Omega}=1,568\ k\Omega=X_C\)
\(X_C=\frac{1}{\omega\cdot C}\Leftrightarrow C=\frac{1}{X_C\cdot \omega}=\frac{1}{2\cdot \pi\cdot f\cdot X_C}=\frac{1}{2\pi\cdot50\ Hz\cdot1,568\ k\Omega}=2\ \mu F\)
Die Ergebnisse sind gleich.
Zusatzaufgabe 7
Es entsteht ein neues Widerstandsdreieck mit den Katheten \(X_{L_p}\) und \(R_p\), wobei \(X_{L_p}\) die Ankathete und \(R_p\) die Gegenkathete des Winkels \(\varphi\) ist.
Überprüfe ob dieses neue Widerstandsdreieck noch immer denselben Phasenverschiebungswinkel \(\varphi\) hat.
Drei mögliche Wege:
1) die Hypotenuse berechnen und \(\sin\varphi\) mit \(R_p\) ausrechnen
2) die Hypotenuse berechnen und \(\cos\varphi\) mit \(X_{L_p}\) ausrechnen
3) \(\tan\varphi\) mit \(R_p\) und \(X{L_p}\) ausrechnen
Hypotenuse \(Z_H\):
\(Z_H=\sqrt{R_p^2+X_{L_p}^2}=4,51\ k\Omega\)
1) \(\varphi=\sin^{-1}\left(\frac{R_p}{Z_H} \right)=69,7°\)
2) \(\varphi=\cos^{-1}\left(\frac{X_{L_p}}{Z_H} \right)=69,7°\)
3) \(\varphi=\tan^{-1}\left(\frac{R_p}{X_{L_p}}\right)=69,7°\)
Der Winkel \(\varphi\) ist immer noch derselbe.