Lernauftrag 14: Leuchstoffröhre
Hier findest du die Aufgaben ohne Lösungen.
Da wir im Rahmen der Wechselstromtechnik und unserer Lernsituation vornehmlich an den grundlegenden Effekten interessiert sind, werden wir uns bezüglich Leuchtstoffröhren ausschließlich auf konventionelle Vorschaltgeräte beschränken. Wir werden nur in einem rechnerischen Vergleich darauf schauen, daß die Alternativen effizienter sind.
Aufgabe 1
Lies im Fachbuch die kurzen Abschnitt 12.1.7 und 12.1.8 zu den Themen Leuchtstofflampe und Vorschaltgeräte.
Aufgabe 2
Dargestellt ist schematisch der Aufbau einer Leuchtstofflampe mit Starter und Vorschaltgerät. Die Leuchtstoffröhre ist zwischen den Fassungen nicht eingezeichnet.
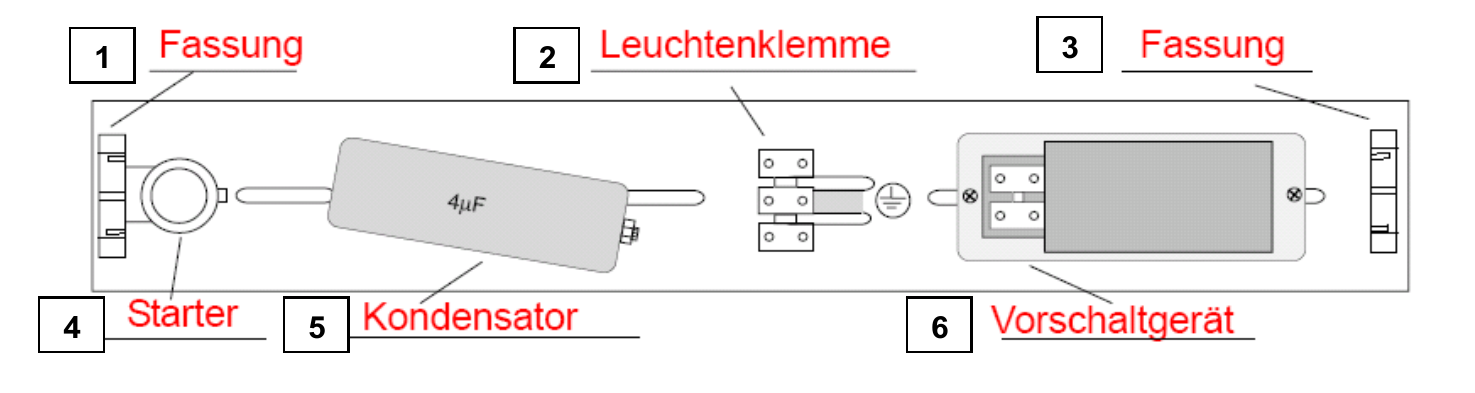
Notiere kurze Erklärungen zu den Aufgaben der Bauteile:
- Leuchtstoffröhre
- Starter
- Vorschaltgerät
- Anschlussklemmen (Leuchtenklemme)
- Fassung
- Kondensator
Aufgabe 3
Dargestellt ist ein Ersatzschaltbild für die Reihenschaltung von Vorschaltgerät und Leuchtröhre. Zusätzlich eingezeichnet sind einige Messgeräte (P1-P6).
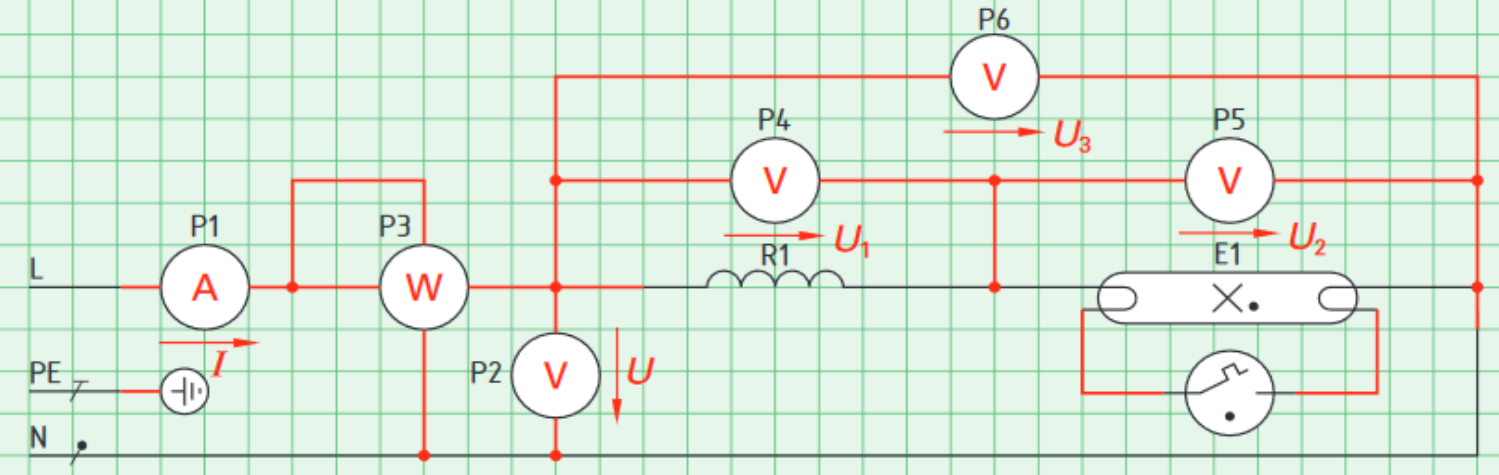
Lies das Schaltbild und versuche Zusammenhänge zwischen den messbaren Größen herzustellen.
Aufgabe 4
Die Leuchtstofflampe hat die Nennbemessungswerte \(230\ V; 58\ W\).
Ausgewählt wurden drei Vorschaltgeräte mit den folgenden Blindleistungen an den Spulen:
1) konventionelles Vorschaltgerät (KVG): \(Q_L=13\ var\)
2) verlustarmes Vorschaltgerät (VVG): \(Q_L=8\ var\)
3) elektronisches Vorschaltgerät (EVG): \(Q_L=4,5\ var\)
Berechne für jedes der drei Vorschaltgeräte in Verbindung mit einer Leuchtstofflampe folgende Größen in der Reihenfolge:
1) Scheinleistung \(S\)
2) Phasenverschiebungswinkel \(\varphi\)
3) Blindspannung \(U_L\)
4) Leistungsfaktor \(\cos \varphi\)
5) Strom \(I\)
6) Impedanz \(Z\)
7) Induktiver Blindwiderstand \(X_L\)
8) Induktivität \(L\) der Spule
Anhand der ersten Berechnungen zum KVG, demonstriere ich einmal die Nutzung von Widerstands-, Spannungs- und Leistungsdreieck, um sich schnell zurecht zu finden.
KVG
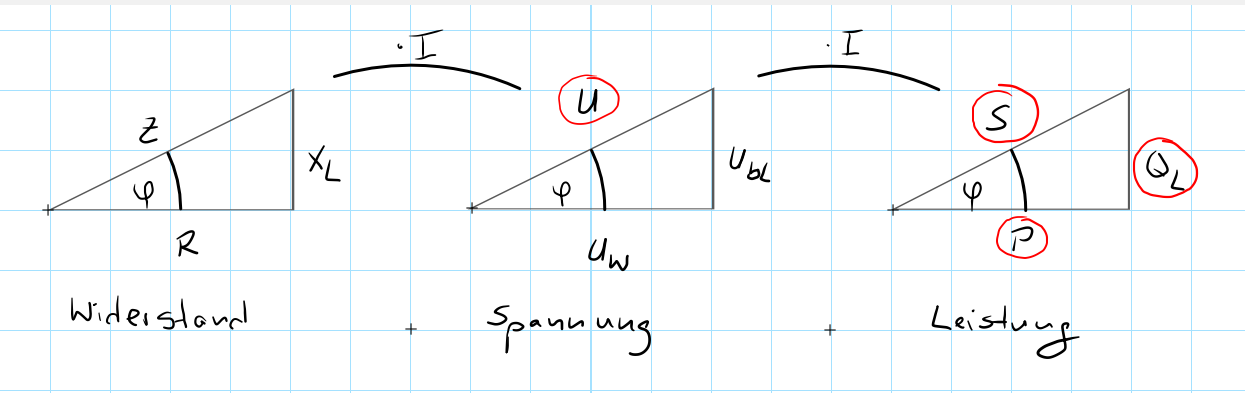
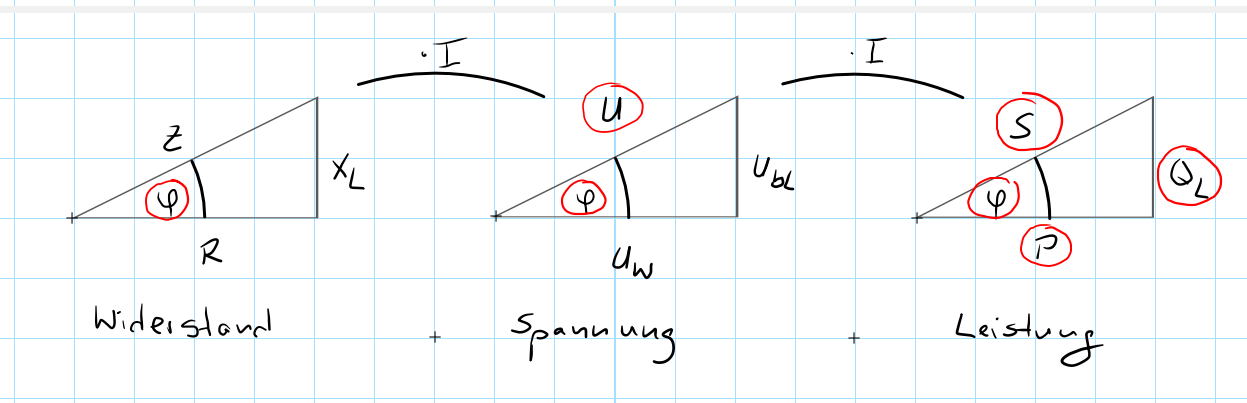
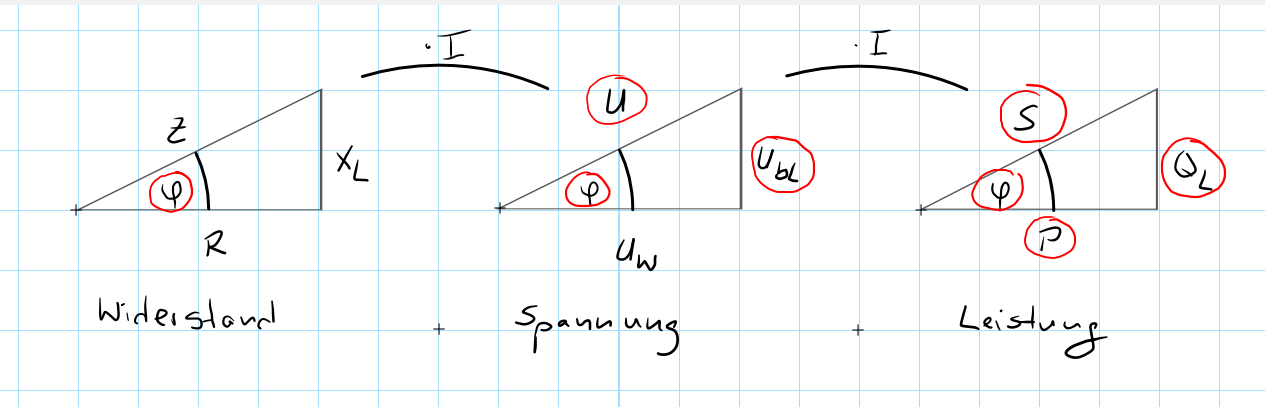
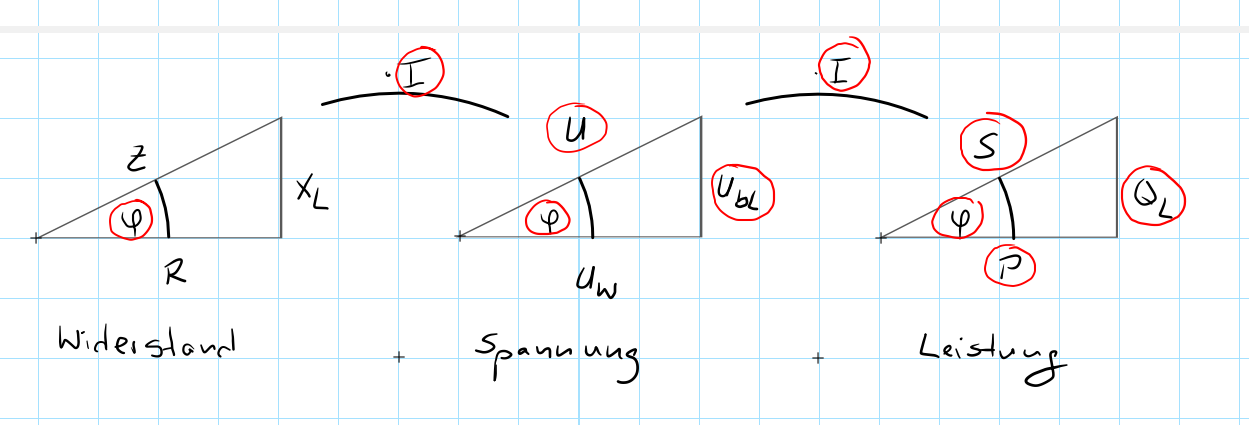
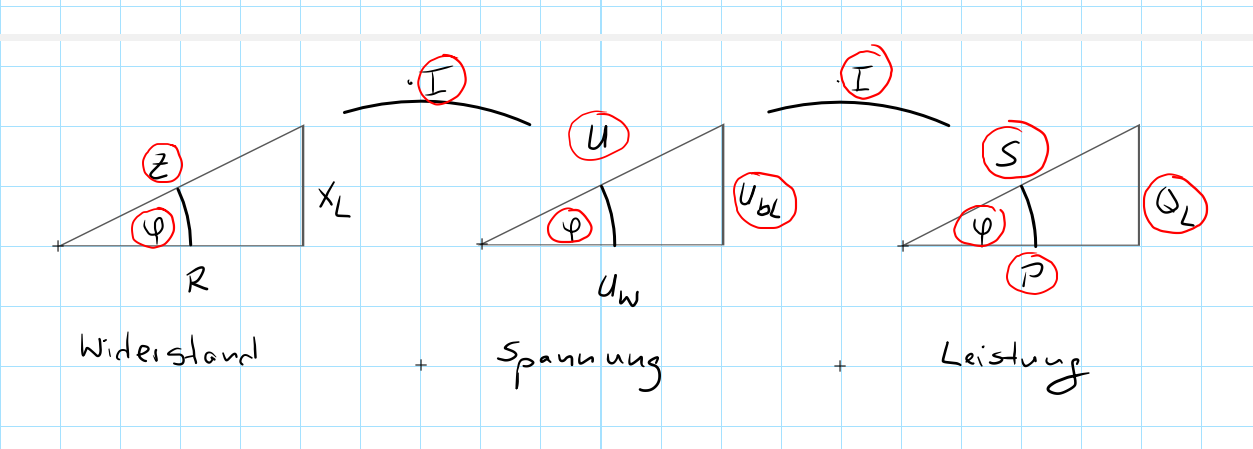
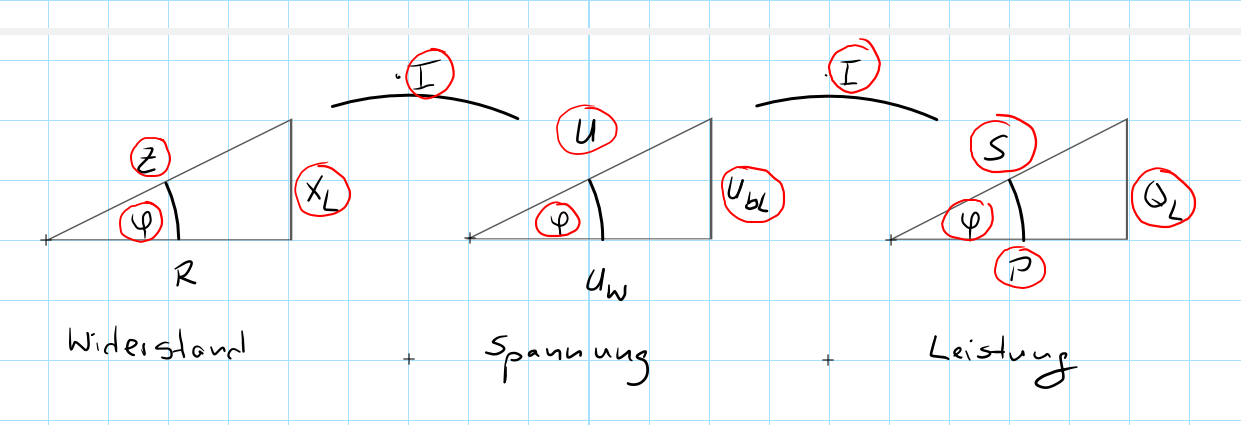
Wir beginnen, indem wir uns zuerst einmal alle drei Dreiecke in der folgenden Form schematisch hinmalen.
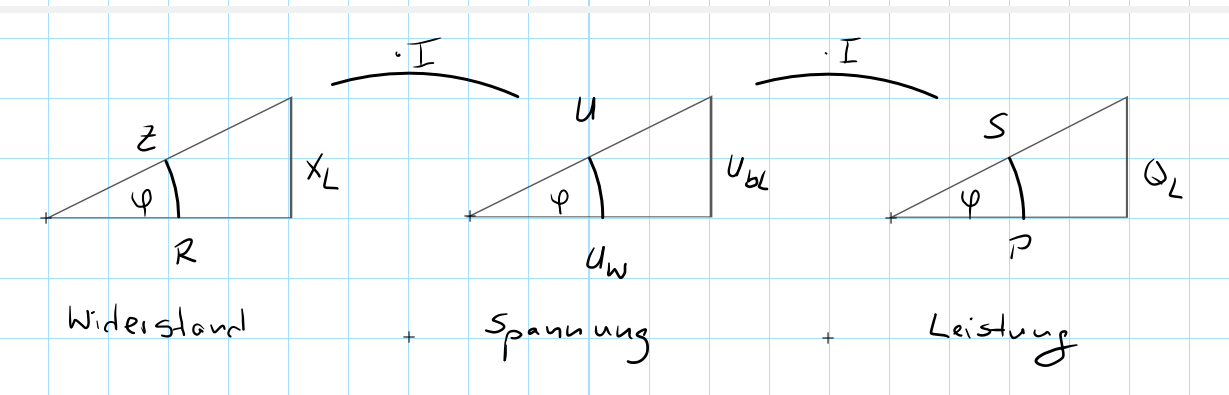
Bemerkungen:
- Alle drei Dreiecke haben denselben Winkel \(\varphi\).
- Die Dreiecke haben ihre Spitze nach oben, da es sich um ein induktives Bauteil (Spule) handelt.
- Die Verhältnisse der Seiten zueinander sind in allen Dreiecken identisch
- Die Anordnung der Dreiecke: Widerstand -> Spannung -> Leistung ist absichtlich gewählt, denn ein Widerstand multipliziert mit dem Strom \(I\) ergibt eine Spannung. Eine Spannung multipliziert mit dem Strom \(I\) ergibt eine Leistung.
- Die Hypotenusen beginnen sprachlich immer mit dem Wort "Schein": Scheinwiderstand \(Z\), Scheinspannung \(U\), Scheinleistung \(S\)
- Die Ankatheten des Winkels \(\varphi\) beginnen sprachlich immer mit dem Wort "Wirk": Wirkwiderstand \(R\), Wirkspannung \(U_W\), Wirkleistung \(P\)
- Die Gegenkatheten des Winkels \(\varphi\) beginnen sprachlich immer mit dem Wort "Blind": Blindwiderstand \(X_L\), Blindspannung \(U_{bL}\) oder auch \(U_L\), Blindleistung \(Q_L\)
Nachdem die Dreiecke gezeichnet sind, vermerken wir uns, welche Größen gegeben sind.
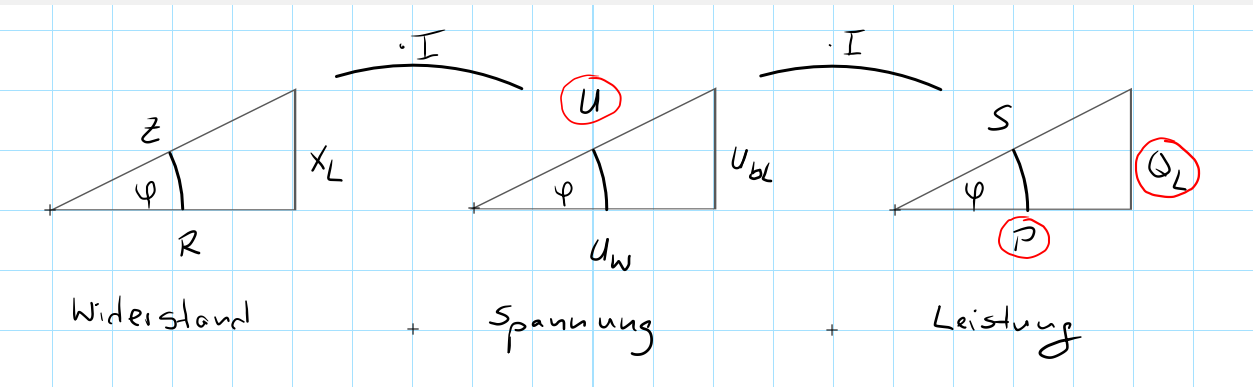
Nach jedem Berechnungsschritt vermerken wir in der Darstellung, welche Größen bekannt sind.
geg: \(U=230\ V, P=58\ W, Q_L=13\ var\)
ges: \(S, \varphi, U_L, \cos \varphi, I, Z, L\)
Lös:
Scheinleistung \(S\):
Ein Blick auf unsere Darstellung zeigt, daß wir im Leistungsdreieck bereits die Größen \(P\) und \(Q_L\) kennen und somit mithilfe des Satzes von Phytagoras die Größe \(Z\) ausrechnen können:
\(S^2=P^2+Q_L^2\Leftrightarrow S=\sqrt{S^2+Q_L^2}=\sqrt{(58\ W)^2+(13\ var)^2}=59,44\ VA\)
Phasenverschiebungswinkel \(\varphi\)
Im Leistungsdreieck sind alle drei Seiten bekannt. Somit haben wir die Wahl, ob wir die Sinusfunktion (Hypotenuse und Gegenkathete) oder die Cosinusfunktion (Hypotenuse und Ankathete) zur Berechnung des Winkels nutzen wollen. Hier werden beide Wege einmal gezeigt:
\(\sin\varphi=\frac{Q_L}{S}\Leftrightarrow \varphi=\sin^{-1}\left(\frac{Q_L}{S}\right)=\sin\left(\frac{13\ var}{59,44\ VA}\right)=12,6°\)
\(\cos\varphi=\frac{P}{S}\Leftrightarrow\varphi=\cos^{-1}\left(\frac{P}{S}\right)=\cos^{-1}\left(\frac{58\ W}{59,44\ VA}\right)=12,6°\)
Blindspannung \(U_L\)
Im Spannungsdreieck ist uns die Hypotenuse \(U\) und der Winkel \(\varphi\) bekannt. Gesucht wird die Gegenkathete des Winkel \(\varphi\). Somit müssen wir die Sinusfunktion verwenden:
\(U_L=U\cdot\sin\varphi=U\cdot\frac{Q_L}{S}=230\ V\cdot\frac{13\ var}{59,44\ VA}=50,3\ V\)
Bemerkung: Es wäre nun ein leichtes mithilfe des Satzes von Phytagoras die Größe \(U_W\) auszurechnen.
Leistungsfaktor \(\cos\varphi\)
Da wir den Cosinus des Winkels \(\varphi\) bestimmen sollen brauchen wir eine Hypotenuse und eine Ankathete. Bisher kennen wir nur im Leistungsdreieck diese Seiten, also nutzen wir \(S\) und \(P\).
\(\cos\varphi=\frac{P}{S}=\frac{58\ W}{59,44\ VA}=0,9758=97,58\%\)
Hinweis: Hier muß die Funktion Cosinus selbst im Taschenrechner nicht angewendet werden. Es reicht \(P\) durch \(S\) zu teilen.
Alternativer Weg: Wir kennen bereits den Winkel \(\varphi\) und können wir die Cosinusfunktion auf auf den Winkel anwenden:
\(\cos\varphi=\cos(12,6°)=0,9759=97,59\%\)
Wir erhalten für unsere Darstellung keine neue Größe:

Strom \(I\)
Um den Strom zu finden, gilt es zwei Dreiecke miteinander zu vergleichen. Der Faktor zwischen den Größen zweier Dreiecke ist immer der Strom \(I\). Bei den bisher bekannten Größen ergeben sich somit zwei Möglichkeiten:
Scheinspannung \(U\) und Scheinleistung \(S\):
\(S=U\cdot I\Leftrightarrow I=\frac{S}{U}=\frac{59,44\ VA}{230\ V}=0,25844\ A=258,44\ mA\)
Blindspannung \(U_L\) und Blindleistung \(Q_L\):
\(Q_L=U_L\cdot I\Leftrightarrow I=\frac{Q_L}{U_L}=\frac{13\ var}{50,3\ V}=0,25844\ A=258,44\ mA\)
Impedanz \(Z\):
Aus dem Widerstandsdreieck kennen wir bisher nur den Winkel \(\varphi\), welcher uns noch nicht viel weiterhilft. Wir nutzen den gefundenen Strom \(I\) und die Scheinspannung \(U\):
\(U=Z\cdot I\Leftrightarrow Z=\frac{U}{I}=\frac{230\ V}{258,44\ mA}=889,95\ \Omega\)
Induktiver Blindwiderstand \(X_L\) der Spule:
Im Widerstandsdreieck sind uns nun Winkel \(\varphi\) und Hypotenuse \(Z\) bekannt. Gesucht ist die Gegenkathete \(X_L\). Somit nutzen wir die Sinusfunktion:
\(\sin\varphi=\frac{X_L}{Z}\Leftrightarrow X_L=\sin\varphi\cdot Z=\sin(12,5°)\cdot 889,95\ \Omega=192,5\ \Omega\)
Bemerkung: Es wäre nun ein leichtes mithilfe des Satzes von Phytagoras die Größe \(R\) auszurechnen.
Induktivität \(L\) der Spule:
Hier helfen uns die Dreiecke nicht weiter. Wir kennen den Blindwiderstand \(X_L\) und wir kennen die Frequenz \(f\) und können somit die Induktivität \(L\) direkt ausrechnen:
\(X_L=\omega\cdot L=2\pi\cdot f\cdot L\Leftrightarrow L=\frac{X_L}{2\cdot\pi\cdot f}=\frac{192,5\ \Omega}{2\pi\cdot 50\ Hz}=0,6127\ H=612,6\ mH\)
Antw: ...
VVG
Die Formeln und Umstellungen bleiben dieselben. Daher ab hier nur noch die Ergebnisse.
geg: \(U=230\ V, P=58\ W, Q_L=8\ var\)
ges: \(S, \varphi, U_L, \cos \varphi, I, Z, L\)
Lös:
\(S=58,55\ VA\)
\(\varphi=7,85°\)
\(U_L=31,43\ V\)
\(\cos\varphi=0,990\)
\(I=254,56\ mA\)
\(Z=903,52\ \Omega\)
\(X_L=123,4\ \Omega\)
\(L=392,8\ mH\)
EVG
geg: \(U=230\ V, P=58\ W, Q_L=4,5\ var\)
ges: \(S, \varphi, U_L, \cos \varphi, I, Z, L\)
\(S=58,17\ VA\)
\(\varphi=4,44°\)
\(U_L=17,79\ V\)
\(\cos\varphi=0,997\)
\(I=252,93\ mA\)
\(Z=909,34\ \Omega\)
\(X_L=70,4\ \Omega\)
\(L=224,1\ mH\)
Aufgabe 5
Zeichne das Zeigerbild der Leistungen für das KVG.
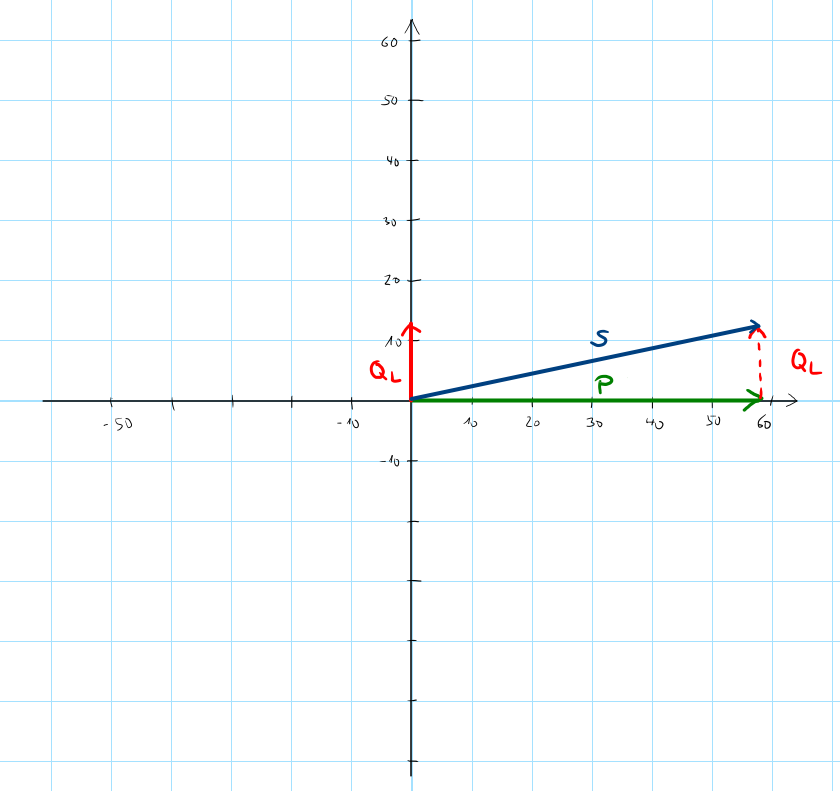
Aufgabe 6
Zeichne das Leistungsdreieck für das KVG.
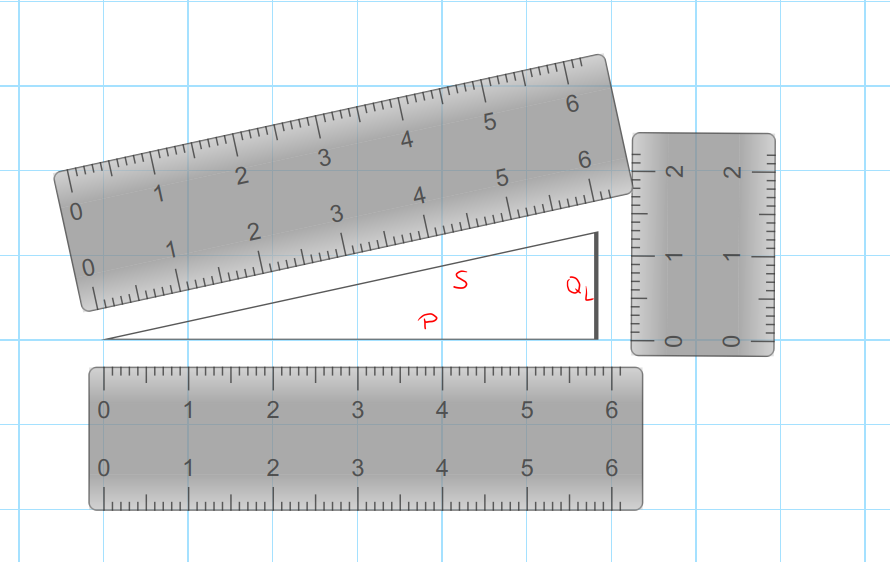
Aufgabe 7
Schau deine berechneten Ergebnisse an und vergleiche die Leistungsfaktoren. Notiere dir eine Erklärung / Bedeutung des Begriffs Leistungsfaktor.
Die Blindleistung sinkt von Aufgabe zu Aufgabe, der Leistungsfaktor steigt von Aufgabe zu Aufgabe.
Ein höherer Leistungsfaktor bedeutet eines geringere Blindleistung. Der Leistungsfaktor gibt an, welcher Anteil der Scheinleistung in Wirkleistung umgesetzt wird.