Lernauftrag 9: Netzinnenwiderstand, Schleifenwiderstand, ...
Hier findest du die Aufgaben ohne Lösungen.
Hinweis vorweg:
Die Begriffe Schleifenwiderstand, Schleifenimpedanz, Fehlerschleifenwiderstand und Fehlerschleifenimpedanz werden hier absichtlich wild durcheinandergeworfen. Sie bezeichnen alle dasselbe Phänomen. Sie werden alle durch das Formelzeichen \(Z_S\) bezeichnet.
Dieselbe Überlegung trifft auf die Begriffe Netzwiderstand, Netzimpedanz, Netzinnenwiderstand und Netzinnenimpedanz zu. Sie werden alle durch das Formelzeichen \(Z_i\) beschrieben.
Unterschied zwischen Widerstand und Impedanz (Scheinwiderstand)
Im Lernfeld 5 haben wir die Abgrenzung von Widerständen und Scheinwiderständen kennengelernt. Widerstände bezeichnen nur den Wirkwiderstand. Scheinwiderstände enthalten sowohl Wirk- als auch Blindwiderstandsanteile. Der Begriff der Impedanz ist das Fachwort für den Scheinwiderstand
Folgerichtig sind in Anlagen mit Wechselspannung die Begriffe Fehlerschleifenimpedanz und Netzimpedanz zu bevorzugen.
Schleifenimpedanz
Um die Einhaltung der Abschaltbedingungen in einer Anlage zu überprüfen ist das Wissen über die Schleifenimpedanz (die Summe aller Widerstände einer geschlossenen Strombahn) notwendig. Nur das Wissen darüber bietet die Möglichkeit bei bekannter Netzspannung den zu erwartenden Fehlerstrom zu ermitteln und mit den gewählten Schutzmaßnahmen abzugleichen, ob die Abschaltbedingungen eingehalten werden.
Die Fehlerstromschleife besteht aus den Widerständen folgender Bestandteile:
- Stromquelle (z.B. Transformator und vorgelagertes Netz)
- dem ungeerdeten aktiven Leiter (Außenleiter), in IT-Systemen zusätzlich der Neutralleiter, bis zur Fehlerstelle
- dem Rückleiter zur Stromquelle
- in TN-Systemen: der Schutzleiter
- in TT-Systemen: der Weg über Anlagenerder -> Erde -> Betriebserder -> Stromquelle
Messort
Die Schleifenimpedanz wird immer am Ende der Kette gemessen, so daß der längstmögliche Leitungsweg berücksichtigt ist. Für Endstromkreise ist das wahlweise die Steckdose oder hinter einer Kabeltrommel.
Gemessen wird die Schleifenimpedanz zwischen Außen- und Schutzleiter (L-PE)
Eine beliebige Verlängerung von Endstromkreisen durch mehrere Verlängerungskabel oder Mehrfachsteckdosen ist unzulässig. Insbesondere Steckverbindungen erhöhen die Impedanz deutlich und können dazu führen, daß die Schleifenimpedanz deutlich steigt.
Aufgabe 1
Gemäß DIN EN 50160 darf in Deutschland die Netzspannung um \(\pm10\%\) von den geforderten \(230\ V\) abweichen. Für die Betrachtung der Schleifenimpedanz ist der niedrigste zulässige Spannungswert der kritische.
Gehen wir von einem Endstromkreis aus, welcher mit einem LS-B16 abgesichert wurde.
Berechne wie hoch die Schleifenimpedanz \(Z_S\) sein darf, damit der LS in jedem Fall unverzögert auslöst.
Hinweis: Mach dir noch einmal klar, welchen Fehlerstrom der LS erfahren muß, damit er in jedem Fall unverzögert auslöst.
geg: \(U=230\ V\pm10\%. I_N=16\ A\)
ges: \(Z_S\)
Lös:
Der Fehlerstrom \(I_K\) für unverzögertes Auslösen in jedem Fall muß mindestens \(I_K=5\cdot I_N=5\cdot 16\ A=80\ A\) betragen.
Dieser stellt sich genau ein, bei:
\(U=Z\cdot I_K\Leftrightarrow Z=\frac{U}{I_K}\)
Somit wird \(I_K\) erreicht für alle Werte Impedanzen \(Z_S\leq Z\), also
\(\Rightarrow Z_S\leq\frac{U}{I_N}\)
Ab hier gibt es zwei Wege:
1) Wir setzen für \(U\) einmal \(U+10\%\) und einmal \(U-10\%\) ein, rechnen aus und nutzen die niedrigere Impedanz \(Z_S\) als den Grenzwert, oder
2) Wir überlegen vorher, ob eine kleinere oder größere Spannung zu einer kleineren Impedanz führen.
Weg 1 ist Fleißarbeit und jedem selbst überlassen. Erklärt wird hier Weg 2:
\(Z_S\) und \(U\) stehen beide im Zähler und sind somit proportional. Ein Verringern von \(U\) führt zum Verringern von \(Z_S\). Da wir den niedrigsten Wert für \(Z_S\) suchen nutzen wir die geringste Spannung, also \(U-10\%\):
\(Z_S\leq\frac{230\ V- 230\ V\cdot10\%}{80 \ A}=\frac{230\ V\cdot0,9}{80\ A}=\frac{207\ V}{80\ A}=2,59\ \Omega\)
Antw: Damit der LS unverzögert auslöst, darf die Schleifenimpedanz maximal \(2,59\ \Omega\) betragen.
Netzimpedanz
Gemessen wird die Netzimpedanz zwischen zwei stromführenden Leitern, also (L-N) oder auch (L1-L2), (L2-L3), (L3-L1)
Im Normalfall steht zu erwarten, daß die Netzimpedanz vom Betrag her der Schleifenimpedanz entspricht. Weichen die Werte deutlich voneinander ab, so liegt ein Fehler in der Anlage vor, welcher genauer ermittelt werden muß. (z.B. zu niedriger Querschnitt des Schutzleiters, Bruch des Schutzleiters, usw.)
Insbesondere in TT-Systemen kann die Messung der Netzimpedanz und der Vergleich gegen die Fehlerschleifenimpedanz aufschlußreich sein, um zu ermitteln ob die Abschaltbedingungen mit dem Anlagenerder zu erreichen sind.
Bewertung des Meßergebnis
Sowohl bei Netzimpedanz \(Z_i\) als auch Schleifenimpedanz \(Z_S\) ist der absolute Betrag zweitrangig. Entscheidend ist den gemessenen Wert als Grundlage zu Ermittlung eines Fehlerstroms zu nutzen und damit abzuschätzen, ob die notwendigen Fehlerströme für zeitgerechte Abschaltung auftreten werden.
Messgeräte haben grundsätzlich Messfehler/-abweichungen. Zulässig sind Abweichungen bis zu 30%.
Entsprechend sollte diese Abweichung immer berücksichtigt werden.
Aufgabe 2: Messabweichung berücksichtigen
In der vorherigen Aufgabe, hatten wir eine Obergrenze für Schleifenimpedanz gefunden. In jedem Fall darf die Impedanz nicht größer werden als dieser Wert. Um nun die \(30\%\) Messabweichung zu berücksichtigen, muß das gefundene Ergebnis um \(30\%\) nach unten korrigert werden.
Berechne wie groß die Schleifenimpedanz unter Berücksichtigung des Messfehlers maximal sein darf.
geg: \(Z_S=2,59\ \Omega\), Messabweichung \(30\%\)
ges: \(Z_{S,\mathrm{korrigiert}}\)
Lös:
Damit das Auslösen des LS unverzögert passiert, darf durch die Messabweichung die Schleifenimpedanz nicht größer als \(Z_S=2,59\ \Omega\) werden. Somit suchen wir die Impedanz \(Z_{S,\mathrm{korrigiert}}\), welche um \(30\%\) vergrößert genau \(Z_S\) ergibt, also:
\(\frac{Z_{S,\mathrm{korrigiert}}}{100\%}=\frac{Z_S}{130\%}\Leftrightarrow Z_{S,\mathrm{korrigiert}}=\frac{Z_S\cdot 100\%}{130\%}=\frac{Z_S}{1,3}=\frac{2,59\ \Omega}{1,3}=2\ \Omega\)
Antw: Die Schleifenimpedanz darf unter Berücksichtigung der Messabweichung maximal \(2\ \Omega\) betragen.
Schlußfolgerung: Wird eine Schleifenimpedanz in der Größenordnung gemessen, dann gilt es immer Maßnahmen zu prüfen, wie diese verringert werden kann.
Aufgabe 3: Zusammenhang Netzimpedanz - Spannungsfall
Aus der Netzimpedanz kann der Spannungsfall abgeleitet werden. Gemessen wurde eine Netzimpedanz von \(2,85\ \Omega\). Abgesichert wurde der Endstromkreis mit einem LS-B16.
1) Berechne den absoluten Spannungsfall, welcher sich aufgrund der Netzimpedanz und des Bemessungsstroms des LS ergibt.
2) Berechne den relativen Spannungsfall.
Beachte: Der hier berechnete Spannungsfall ist der Spannungsfall von Transformator bis Verbraucher.
geg: \(Z_i=2,85\ \Omega, U_0=230\ V, I_N=16\ A\)
ges: \(\Delta U, \Delta u\)
Lös:
\(\Delta U=Z_i\cdot I_N=2,85\ \Omega\cdot 16\ A=45,6\ V\)
\(\Delta u=\frac{\Delta U}{U_0}\cdot 100\%=\frac{45,6\ V}{230\ V}\cdot 100\%=19,83\%\)
Der Spannungsfall beträgt \(20\%\).
Aufgabe 4: Netzimpedanzen zur Spannungsfallbeurteilung nutzen
Die Netzimpedanz an unterschiedlichen Stelle zu messen führt dazu, daß Spannungsfälle sinnvoll bewertet werden können.
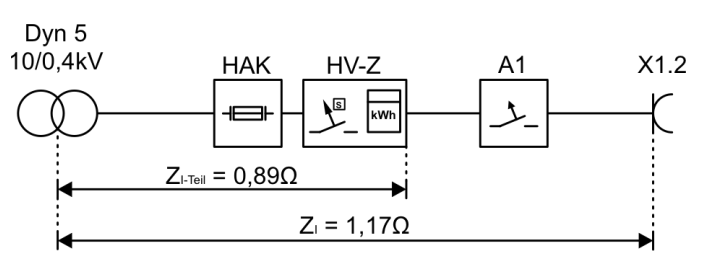
An der Steckdose X1.2 wurde eine Netzimpedanz \(Z_i=1,17\ \Omega\) und an den Abgangsklemmen der zugehörigen Messeinrichtung im Hauptverteiler eine Teilnetzimpedanz \(Z_{i\mathrm{-Teil}}=0,89\ \Omega\) gemessen. Der Endstromkreis 1 wurde mit einem LS-B16 abgesichert.
Berechne den Spannungsfall des Endstromkreises und bewerte, ob er nach DIN 18015-1 zuässig ist.
geg: \(U_0=230\ V, Z_i=1,17\ \Omega, Z_{i\mathrm{-Teil}}=0,89\ \Omega, I_N=16\ A\)
ges: \(\Delta U, \Delta u\)
Lös:
\(Z_\mathrm{Ltg}=Z_i-Z_{i\mathrm{-Teil}}=1,17\ \Omega-0,89\ \Omega=0,28\ \Omega\)
\(\Delta U=Z_\mathrm{Ltg}\cdot I_N=0,28\ \Omega\cdot 16\ A=4,48\ V\)
\(\Delta u=\frac{\Delta U}{U_0}\cdot 100\%=\frac{4,48\ V}{230\ V}\cdot 100\%=1,95\%\)
Antw: Der Spannungsfall beträgt \(4,48\ V\) und ist mit \(\Delta u =1,95\%\leq3\%\) ist zulässig.
Aufgabe 5
Anstelle der Steckdose X1.2 aus Aufgabe 4 befindet sich nun eine Herdanschlussdose. Der Herd wird mit Wechselspannung versorgt und sollte mit einem LS-B25 abgesichert werden. Die gemessenen Netzimpedanzen entsprechen der Aufgabe 4.
Berechne für diese Situation den Spannungsfall des Endstromkreises und bewerte, ob er nach DIN 18015-1 zulässig ist.
geg: \(U_0=230\ V, Z_\mathrm{Ltg}=0,28\ \Omega, I_N=25\ A\)
ges: \(\Delta U, \Delta u\)
Lös:
\(\Delta U=Z_\mathrm{Ltg}\cdot I_N=0,28\ \Omega\cdot 25\ A=7\ V\)
\(\Delta u=\frac{\Delta U}{U_0}\cdot 100\%=\frac{7\ V}{230\ V}\cdot100\%=3,04\%\)
Antw: Der Spannungsfall beträgt \(7\ V\) und ist mit \(\Delta = 3,04\%>3\%\) nicht zulässig. Der Leitungswiderstand \(Z_i\) muß verkleinert werden indem der Querschnitt der Leitung erhöht wird.
Hier geht es zum nächsten Lernauftrag.