Lernauftrag 12: Leistungsdreieck
Hier findest du die Aufgaben ohne Lösungen.
Aufgabe 1
Erstelle eine Übersicht über den Zusammenhang zwischen Wirk-, Blind- und Scheinleistung. Stelle dabei insbesondere die Analogien zu Spannungs- und Widerstandsdreieck heraus.
Fachbuch S. 142
Aufgabe 2
Eine Spule wird an eine Gleichspannungsquelle geschaltet, welche eine konstante Spannung von \(U=100\ V\) bereitstellt. Gemessen wurde der Strom, welcher durch die Spule fließt. Dieser beträgt \(I=5\ A\).
Anschließend wird eine Wechselspannung mit der Frequenz \(50\ Hz\) angelegt und solange reguliert, bis erneut ein Strom von \(I=5\ A\) durch die Spule fließt. Die notwendige Wechselspannung dafür beträgt \(230\ V\).
Berechne folgende Werte in dieser Reihenfolge:
1) Wirkwiderstand \(R\)
\(U=R\cdot I\Leftrightarrow R=\frac{U}{I}=\frac{100\ V}{5\ A}=20\ \Omega\)
1) Scheinwiderstand \(Z\)
\(U=Z\cdot I\Leftrightarrow Z=\frac{U}{I}=\frac{230\ V}{5\ A}=46\ \Omega\)
2) Phasenverschiebungswinkel \(\varphi\)
\(R = Z\cdot \cos(\varphi)\Leftrightarrow \cos(\varphi)=\frac{R}{Z}\Leftrightarrow \varphi = \cos^{-1}\left(\frac{R}{Z}\right)=\cos^{-1}\left(\frac{20\ \Omega}{46\ \Omega}\right)=64,23°\)
3) induktiver Blindwiderstand \(X_L\)
Zwei Möglichkeiten:
Satz des Phytagoras:
\(Z^2=R^2+X_L^2\Leftrightarrow X_L=\sqrt{Z^2-R^2}=\sqrt{(46\ \Omega)^2-(20\ \Omega)^2}=41,42\ \Omega\)
Winkelfunktionen:
\(X_L=Z\cdot\sin(\varphi)=46\ \Omega\cdot\sin(64,23°)=41,42\ \Omega\)
4) Induktivität \(L\)
\(X_L=\omega\cdot L\Leftrightarrow L=\frac{X_L}{\omega}=\frac{X_L}{2\cdot\pi\cdot f}=\frac{41,42\ \Omega}{2\cdot\pi\cdot 50\ Hz}=0,13184\ H=131,84\ mH\)
Aufgabe 3
Zeichne das Widerstandsdreieck zu Aufgabe 2.
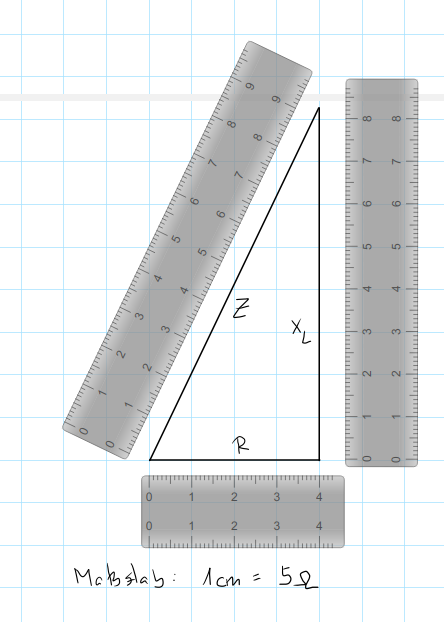
Aufgabe 4
Berechne die Scheinleistung \(S\), die Wirkleistung \(P\) und die induktive Blindleistung \(Q_L\).
geg: \(U=230\ V, I=5\ A, \varphi=64,23°, U_W=100\ V\)
Die Scheinleistung \(S\) erhalten wir über die Wechselspannung / Scheinspannung \(U\) und den Strom \(I\):
\(S=U\cdot I=230\ V\cdot 5\ A=1150\ W=1,15\ kW\)
Die Wirkleistung \(P\) können wir auf zwei Wegen ausrechnen.
a) Wir nutzen die Wirkspannung \(U_W\) und den Strom \(I\)
b) Wir nutzen die Scheinleistung \(S\) und den Phasenverschiebungswinkel \(\varphi\)
a) \(P=U_W\cdot I=100\ V\cdot 5\ A=500\ W\)
b) \(P=\cos\varphi\cdot S=\cos(64,23°)\cdot 1,15\ kW=499,97\ W=500\ W\)
Die Blindleistung \(Q_L\) können wir nun auf zwei Wegen ausrechnen.
a) Satz des Pythagoras im Leistungsdreieck nutzen, da wir die Seiten \(S\) und \(P\) kennen
b) Wir nutzen die Scheinleistung \(S\) und den Phasenverschiebungswinkel \(\varphi\)
a) \(S^2=P^2+Q_L^2\Leftrightarrow Q_L=\sqrt{S^2-P^2}=\sqrt{(1,15\ kW)^2-(500\ W)^2}=1035\ W=1,04\ kW\)
b) \(Q_L=\sin\varphi\cdot S=\sin(64,23°)\cdot 1,15\ kW=1035,6\ W=1,04\ kW\)
Aufgabe 5
Zeichne das Leistungsdreieck zu Aufgabe 4.
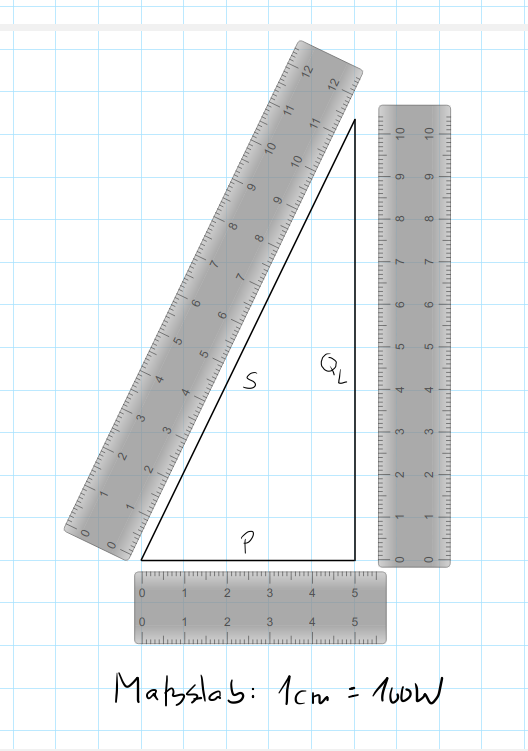
Aufgabe 6
Auf dem Bildschirm eines Oszilloskops sind die Kennlinien der Spannungen \(U_{L}\) (auch \(U_{bL}\) genannt) und \(U_R\) (auch \(U_W\) genannt) der Widerstandsschaltung abgebildet.
Das Oszilloskop ist in der Vertikalablenkung \(\mathbf{5V/Div}\) und in der Horizontalablenkung mit \(\mathbf{5\mu s/Div}\) eingestellt.
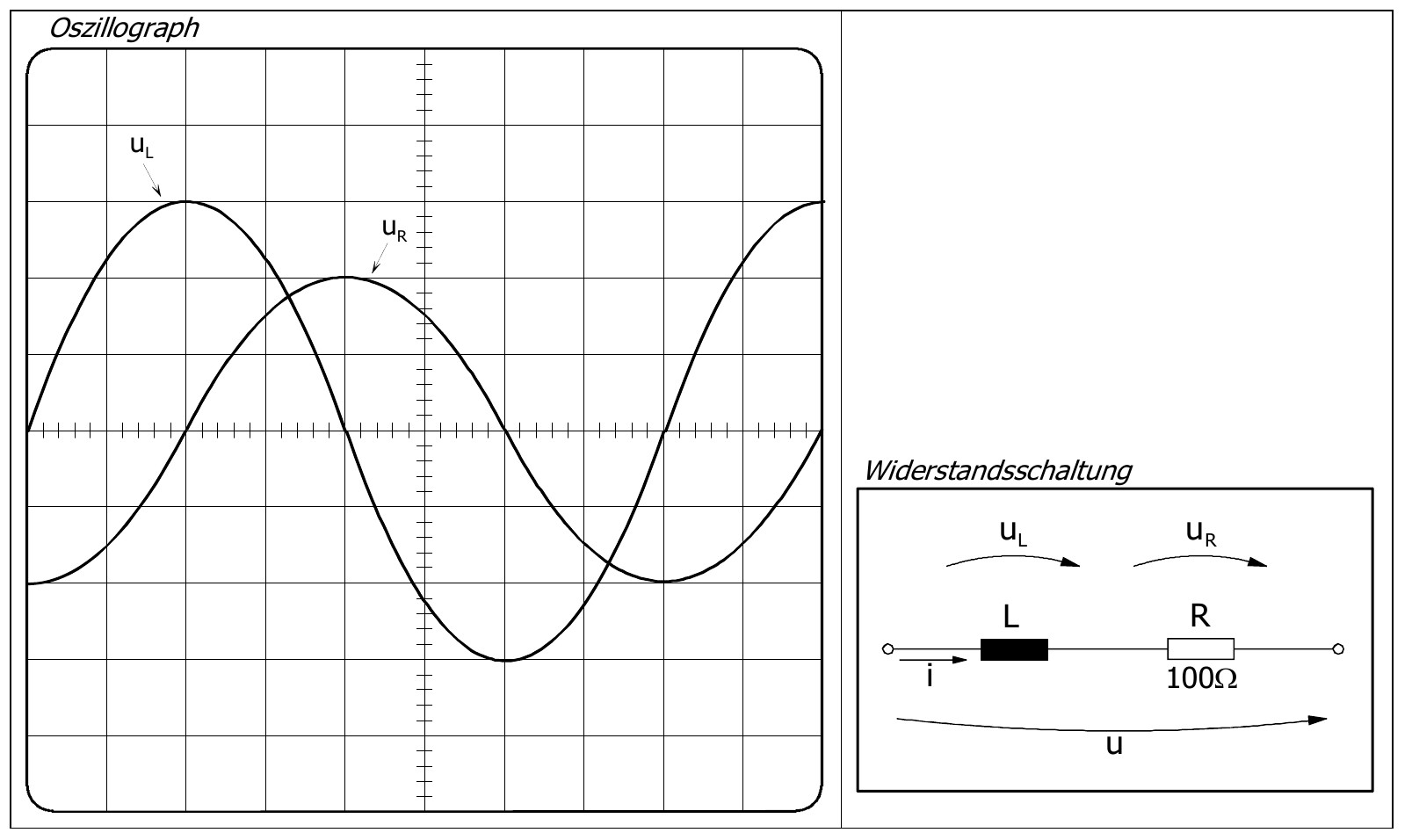
Gesucht sind die folgenden Werte. Entscheide selbst, ob du sie aus dem Oszillogramm ablesen kannst oder berechnen mußt.
1) Phasenwinkel \(\varphi\) zwischen den Spannungen \(U_L\) und \(U_R\)
Zeitverschiebung ablesen
\(U_L\) läuft \(U_R\) voraus, 2 Div Abstand \(\Rightarrow 2\ Div \cdot 5\frac{\mu s}{Div}=10\mu s\)
Periode ablesen
\(T=8\ Div\cdot 5\frac{\mu s}{Div}=40\mu s\)
Verhältnis aufstellen:
\(\frac{360°}{40\mu s}=\frac{\varphi}{10\mu s}\Leftrightarrow \varphi=\frac{360°\cdot10\mu s}{40\mu s}=90°\)
2) Spitzenwert der Wechselspannungen \(U_L\) und \(U_R\)
Ablesen:
\(\hat U_L=3\ Div\cdot 5\frac{V}{Div}=15\ V\)
\(\hat U_R=2\ Div\cdot 5\frac{V}{Div}=10\ V\)
3) Effektivwert der Wechselspannungen \(U_L\) und \(U_R\)
Ausrechnen mithilfe der Spitzenwerte
\(U_L=\frac{\hat U_L}{\sqrt 2}=\frac{15\ V}{\sqrt 2}=10,6\ V\)
\(U_R=\frac{\hat U_R}{\sqrt 2}=\frac{10\ V}{\sqrt 2}=7,07\ V\)
4) Gesamtspannung \(U\)
Spannungen in Reihe werden addiert
\(U=\sqrt{U_L^2+U_R^2}=\sqrt{(10,6\ V)^2+(7,07\ V)^2}=12,74\ V\)
5) Strom \(I\)
Strom in Reihe bleibt identisch. \(R=100\ \Omega\), \(U_R\) und Ohmsches Gesetz nutzen
\(U_R=R\cdot I\Leftrightarrow I=\frac{U_R}{R}=\frac{7,07\ V}{100\ \Omega}=70,7\ mA\)
6) Phasenwinkel \(\varphi\) zwischen der Gesamtspannung \(U\) und dem Strom \(I\)
Zwei Möglichkeiten:
\(\sin(\varphi)=\frac{U_L}{U}\Leftrightarrow \varphi=\sin^{-1}\left(\frac{U_L}{U}\right)=\sin^{-1}\left(\frac{10,6\ V}{12,74\ V}\right)=56,3°\)
\(\cos(\varphi)=\frac{U_R}{U}\Leftrightarrow \varphi=\cos^{-1}\left(\frac{U_W}{U}\right)=\cos^{-1}\left(\frac{7,07\ V}{12,74\ V}\right)=56,3°\)
7) Frequenz der Wechselspannungen
\(f=\frac{1}{T}=\frac{1}{40\mu s}=25\ kHz\)
8) Induktiver Blindwiderstand \(X_L\)
Zwei Möglichkeiten:
\(X_L=\frac{U_L}{I}=\frac{10,6\ V}{70,7\ mA}=149,9\ \Omega\)
\(\cos\varphi=\frac{R}{Z}\Leftrightarrow Z=\frac{R}{\cos\varphi}=181,2\ \Omega\)
\(Z^2=R^2+X_L^2\Leftrightarrow X_L=\sqrt{Z^2-R^2}=\sqrt{(181,2\ \Omega)^2-(100\ \Omega)^2}=151,2\ \Omega\)
9) Induktivität \(L\) der Spule
\(X_L=\omega\cdot L\Leftrightarrow L=\frac{X_L}{\omega}=\frac{X_L}{2\cdot\pi\cdot f}=\frac{151,2\ \Omega}{2\cdot \pi \cdot 25\ kHz}=0,63662\ H=636,62\ mH\)
Aufgabe 7
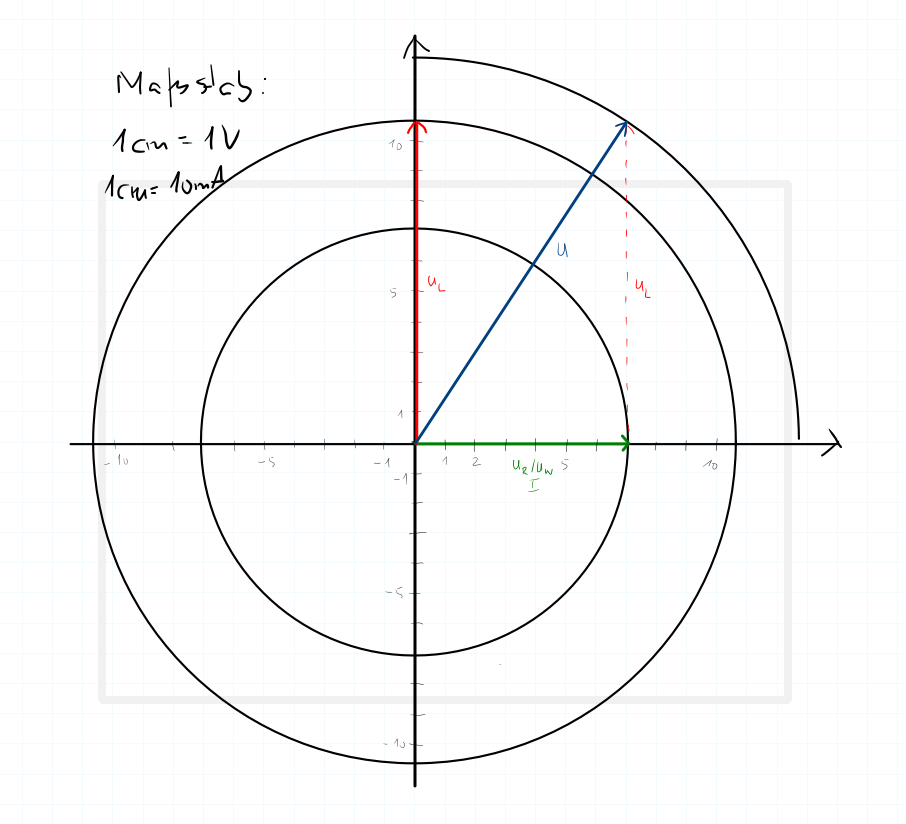
Zeichne das Zeigerdiagramm der Spannungen und des Stroms nach einem frei gewählten Maßstab.