09 - Logische Grundfunktionen recherchieren
Hier findest die Aufgaben ohne Lösungen.
Dualzahlen besitzen den Vorteil, daß die Zahlen 0 und 1 auch anders interpretiert werden können. So zum Beispiel:
- 0 = Taster ungedrückt = Falsch = Spannungsfrei = low
- 1 = Taster gedrückt = Wahr = Steuerspannung = high
Kennengelernt hatten wir in Bezug auf Schützschaltungen bereits die Reihen- und Parallelschaltung von Tastern. Mehrfach erwähnt wurde, daß diese Schaltungen logischen Verknüpfungen entsprechen.
Ermittle in den folgenden Aufgaben zu dem Stromlaufplan die Wertetabelle, die logische Grundfunktion, das Schaltzeichen und die Funktionsgleichung.
Aufgabe 1
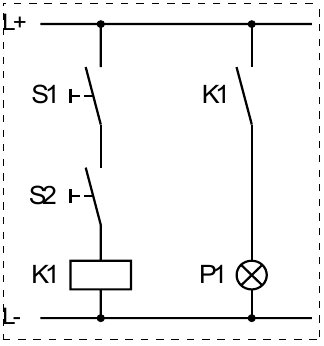
| S2 | S1 | P1 |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
logische Grundfunktion: UND
Funktionsgleichung: \(P1 = S1\land S2\)
Schaltzeichen: Siehe Tabellenbuch S. 355
Aufgabe 2
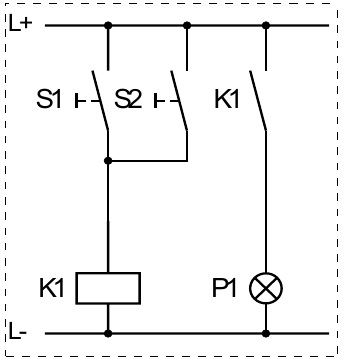
| S2 | S1 | P1 |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
logische Grundfunktion: ODER
Funktionsgleichung: \(P1=S1\lor S2\)
Schaltzeichen: Siehe Tabellenbuch S. 355
Aufgabe 3
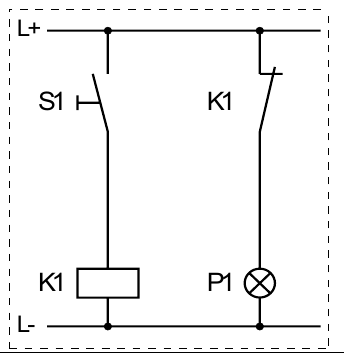
| S1 | P1 |
|---|---|
| 0 | 1 |
| 1 | 0 |
logische Grundfunktion: NICHT (Negation)
Funktionsgleichung: \(P1=\overline{S1}\)
Schaltzeichen: Siehe Tabellenbuch S. 355
Aufgabe 4
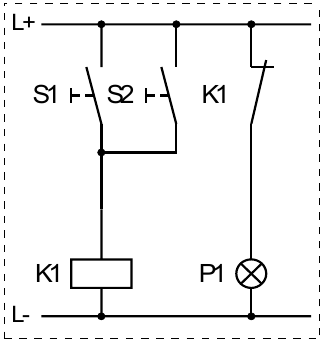
| S2 | S1 | P1 |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 0 |
logische Grundfunktion: NICHT-ODER (NOR)
Funktionsgleichung: \(P1=S1\overline\lor S2\) oder \(P1=\overline{(S1\lor S2)}\)
Schaltzeichen: Siehe Tabellenbuch S. 355
Aufgabe 5
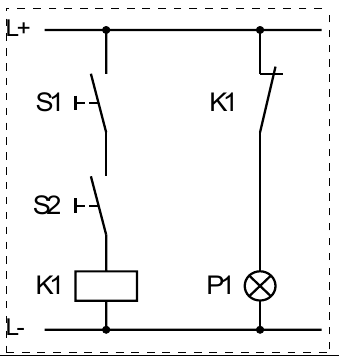
| S2 | S1 | P1 |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
logische Grundfunktion: NICHT-UND (NAND)
Funktionsgleichung: \(P1=S1\overline\land S2\) oder \(P1=\overline{(S1\land S2)}\)
Schaltzeichen: Siehe Tabellenbuch S. 355
Aufgabe 6
Ergänze das folgende Glossar an logischen Funktionszeichen mit der jeweiligen Bedeutung und dem Schaltzeichen.
- \(x=a \lor b\)
- \(x=a\land b\)
- \(x=a\overline{\land} b\)
- \(x=a\overline{\lor}b\)
- \(x=\overline a\)
- \(x=\lnot a\)
- \(x=a\rightarrow b\)
- \(x=a\leftrightarrow b\)
- \(x=a\nleftrightarrow b\)
Siehe Tabellenbuch S. 355
Aufgabe 7
Recherchiere was die Begriffe Disjunktion und Konjunktion bedeuten.
Weiter zur nächsten Lernaufgabe