Spannungsfall
Hier findest du die Aufgaben ohne Lösungen.
Aufgabe 1: Notwendigkeit der Spannungsfallbegrenzung
Begründe warum es der maximal zulässige Spannungsfall in der Elektroinstallation vorgeschrieben ist.
Die Einhaltung des zulässigen Spannungsfalls dient der Verringerung von Verlusten auf Leitungen. Außerdem wird dadurch gewährleistet, dass Verbrauchsmittel mit einer ausreichend hohen Spannung versorgt werden können.
Aufgabe 2: Spannungsfall im Wechselstromsystem
Am Berliner TN-System ist ein Elektroherd mit einer Bemessungsleistung von \(5,5\ kW\) über eine Leitung NYIF \(3\times 2,5\ mm^2\) angeschlossen.
1) Wie lang darf die Leitung maximal sein, um den nach DIN 18015-1 zulässigen Spannungsfall einzuhalten?
2) Ermittle den Bemessungsstrom des Leitungsschutzschalters, mit dem dieser Stromkreis abgesichert werden muss.
3) Welche höchstzulässige Leitungslänge ist laut Tabelle "maximale Leitungslängen" (siehe Infoblatt) zu beachten?
4) Erläutere mögliche Abweichungen zwischen den berechneten und abgelesenen Leitungslängen.
5) Welcher Leiternennquerschnitt ist zu verlegen, um bei einer erforderlichen Leitungslänge von \(25\ m\) den zulässigen Spannungsfall nicht zu überschreiten.
geg: \(\epsilon=3\%, U=230\ V, P=5,5\ kW, A=2,5\ mm^3\)
1. Maximale Leitungslänge
\(\epsilon=\frac{\Delta U\cdot100\%}{U}\Leftrightarrow \Delta U=\frac{\epsilon\cdot U}{100\%}=\frac{3\%\cdot230\ V}{100\%}=6,9\ V\)
\(\Delta U=\frac{2\cdot P\cdot l}{A\cdot\gamma\cdot U}\Leftrightarrow l=\frac{\Delta U\cdot \gamma\cdot A\cdot U}{2\cdot P}=\frac{6,9\ V\cdot56\ \frac{m}{\Omega\cdot mm^2}\cdot 2,5\ mm^2\cdot 230\ V}{2\cdot 5,5\ kW}=20,2\ m\)
2. \(I_N\) des LS
\(P=U\cdot I\Leftrightarrow I=\frac{P}{U}=\frac{5,5\ kW}{230\ V}=23,9\ A\)
Es wird ein LS mit \(I_N=25\ A\) gewählt.
3. Leitungslänge nach Tabelle
Nach Tabelle ergibt sich \(l_\mathrm{max}=19,3\ m\)
4. Abweichungen
Der aus der Tabelle abgelesene Wert berücksichtigt den Bemessungsstrom des LS-Schalters, während der berechnete Wert sich aus dem Bemessungsstrom des Elektroherdes ergibt.
5. Leiternennquerschnitt
\(\Delta U=\frac{2\cdot P\cdot l}{\gamma\cdot A\cdot U}\Leftrightarrow A=\frac{2\cdot P\cdot l}{\Delta U\cdot \gamma\cdot U}=\frac{2\cdot 5,5\ kW\cdot 25\ m}{6,9\ V\cdot 56\ \frac{m}{\Omega\cdot mm^2}\cdot 230\ V}=3,1\ mm^2\)
\(\Rightarrow A=4\ mm^2\)
Aufgabe 3: Physikalischer Hintergrund
Wovon hängt der Spannungsfall auf einer Leitung ab? Kreuze die vollständig richtige Antwort an.
- [ ] nur vom Widerstand der Leitung und vom Leiterquerschnitt
- [ ] nur von der Leiterlänge und vom Leiterquerschnitt
- [ ] nur von der Leitfähigkeit und vom spezifischen Widerstand
- [ ] nur vom Leiterwerkstoff und vom Isolierwerkstoff
- [?] vom Widerstand der Leitung und von der Stromstärke
Aufgabe 4: Grenzwerte
Welcher Spannungsfall darf auf der Leitung zwischem dem Hausanschlusskasten und dem Zählerplatz bei einer Leistung von \(150\ kVA\) nicht überschritten werden? Kreuze die richtige Antwort an.
- [ ] A: 0,5%
- [?] B: 1%
- [ ] C: 1% bis 1,5%
- [ ] D: 3%
- [ ] E: 4%
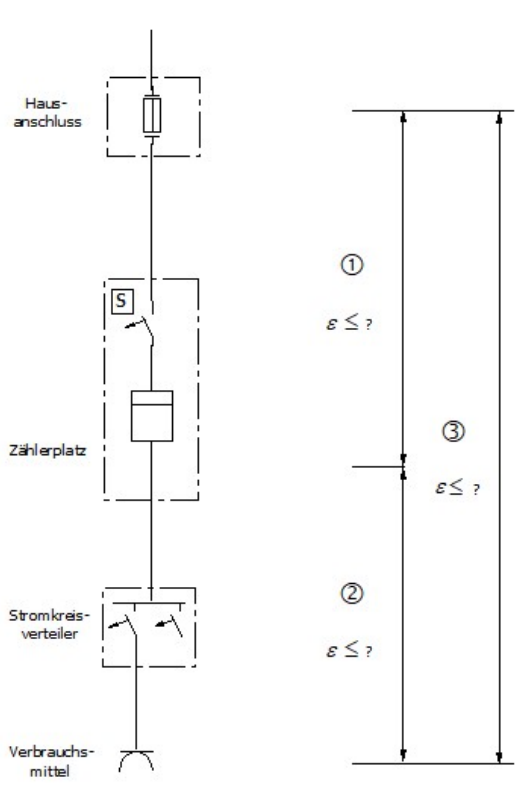
Um eine einwandfreie Funktion angeschlossener Geräte zu gewährleisten, darf der Spannungsfall bestimmte Grenzwerte nicht überschreiten. Kreuze die Zeile an, in der die einzuhaltenden Werte für einen Leistungsbedarf unter \(100\ kVA\) für die abgebildete Anlage korrekt angegeben sind.
- [ ] A: \(\fbox{1} \leq 3\%, \fbox{2} \leq 0,5\%, \fbox{3}\leq0,5\%\)
- [ ] B: \(\fbox{1} \leq 1,5\%, \fbox{2} \leq 3\%, \fbox{3}\leq4\%\)
- [ ] C: \(\fbox{1} \leq 0,5\%, \fbox{2} \leq 3\%, \fbox{3}\leq3,5\%\)
- [?] D: \(\fbox{1} \leq 0,5\%, \fbox{2} \leq 3\%, \fbox{3}\leq4\%\)
- [ ] E: \(\fbox{1} \leq 1,25\%, \fbox{2} \leq 3\%, \fbox{3}\leq4,25\%\)
Aufgabe 5: Spannungsfall in einer Installationsanlage

1) Berechne für abgebildete Elektroinstallation, ob der nach DIN VDE 0100-520 vorgeschriebene prozentuale Spannungsfall eingehalten wird.
2) Überprüfe mittels der Tabelle "maximale Leitungslänge", ob die höchstzulässige Leitungslängen \(l_1\) bis \(l_3\) eingehalten werden.
1. Spannungsfall
\(\Delta U_1=\frac{\sqrt{3}\cdot I\cdot l\cdot\cos\varphi}{\gamma\cdot A}=\frac{\sqrt{3}\cdot80\ A\cdot15\ m\cdot 1}{56\ \frac{m}{\Omega\cdot mm^2}\cdot 25\ mm^2}=1,48\ V\)
\(\varepsilon_1=\frac{\Delta U_1\cdot 100\%}{U}=\frac{1,48\ V\cdot100\%}{400\ V}=0,37\%\)
\(\Delta U_2=\frac{\sqrt{3}\cdot I\cdot l\cdot\cos\varphi}{\gamma\cdot A}=\frac{\sqrt{3}\cdot 50\ A\cdot 25\ m\cdot 1}{56\ \frac{m}{\Omega\cdot mm^2}\cdot 10\ mm^2}=3,8\ V\)
\(\varepsilon_2=\frac{\Delta U_2\cdot 100\%}{U}=\frac{3,8\ V\cdot 100\%}{400\ V}=0,95\%\)
\(\Delta U_3=\frac{2\cdot I\cdot l\cdot\cos\varphi}{\gamma\cdot A}=\frac{2\cdot16\ A\cdot 20\ m\cdot 1}{56\ \frac{m}{\Omega\cdot mm^2}\cdot 1,5\ mm^2}=7,6\ V\)
\(\varepsilon_3=\frac{\Delta U_3\cdot 100\%}{U}=\frac{7,6\ V\cdot 100\%}{230\ V}=3,3\%\)
\(\varepsilon=\varepsilon_1+\varepsilon_2+\varepsilon_3=0,37\%+0,95\%+3,3\%=4,62\%\)
Der nach DIN VDE 0100-520 vorgeschriebene Spannungsfall von \(4\%\) ist nicht eingehalten.
2. maximale Leitungslängen
\(l_1=20,2\ m\) => maximale Leitungslänge eingehalten
\(l_2=13,0\ m\) => maximale Leitungslänge eingehalten
\(l_3=18,1\ m\) => maximale Leitungslänge nicht eingehalten
Aufgabe 6: Spannungsfall bei Kleinspannung
Am Ende einer \(1,9\ m\) langen Kupferleitung sollen drei \(12\ V\)-Halogenglühlampen mit einer Leistung von je \(35\ W\) betrieben werden. Vom Beleuchtungsplaner wird eine relative Lichtstromminderung von maximal \(5\ \%\) vorgegeben.
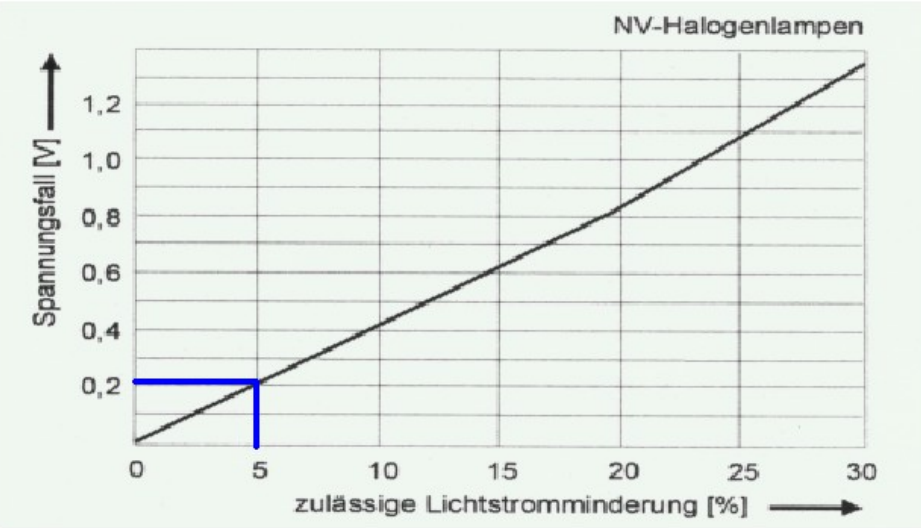
1) Ermittle mithilfe des Diagramms, wie hoch der Spannungsfall ist, welcher zu einer Lichtminderung von \(5\ \%\) führt.
2) Berechne den Leiternennquerschnitt, der nach diesen beleuchtungstechnischen Gesichtspunkten zu wählen ist.
1. Spannungsfall mit Diagramm
Laut Diagramm beträgt der Spannungsfall bei einer Lichtstromminderung von \(5\%\) => \(\Delta U=0,2\ V\)
2. Leiterquerschnitt
\(\Delta U=\frac{2\cdot P\cdot l}{\gamma\cdot A\cdot U}\Leftrightarrow A=\frac{2\cdot P\cdot l}{\Delta U\cdot \gamma\cdot U}=\frac{2\cdot 105\ W\cdot 1,9\ m}{0,2\ V\cdot 56\ \frac{m}{\Omega\cdot mm^2}\cdot 12\ V}=2,9\ mm^2\)
Aus beleuchtungstechnischer Sicht ist ein Leiterquerschnitt von \(4\ mm^2\) zu verlegen.
Aufgabe 7
In Aufgabe 6 und 7 des vorherigen Lernauftrages wurde bereits der Strom und der Bemessungsquerschnitt für einen Durchlauferhitzer im Drehstromsystem (\(400\ V/ 50\ Hz\)) mit einer Leistungsaufnahme von \(21\ kW\) betrachtet.
Der Durchlauferhitzer ist mit einer \(14\ m\) langen Leitung angeschlossen. Der Spannungsfall darf \(3\ \%\) nicht überschreiten
Berechne wie hoch der absolute Spannungsfall ist.
geg: \(U=400\ V, \Delta u=3\%\)
ges: \(\Delta U\)
Lös: \(\Delta u=3\%\) von \(U=400\ V\) sind \(\Delta U=12\ V\)
Antw: Der absolute Spannungsfall beträgt \(\Delta U =12\ V\)
Aufgabe 8
Berechne nun mithilfe des gefundenen Stroms, des absoluten Spannungsfalls, der Leitungslänge und des Materials wie groß der Querschnitt mindestens sein muß.
geg: \(\Delta U=12\ V, \gamma=56\ \frac{m}{\Omega\cdot mm^2}, l=14\ m, I=30,4\ A, \cos\varphi=1\)
ges: \(A\)
Lös: \(A=\frac{\sqrt{3}\cdot I\cdot l\cdot \cos\varphi}{\gamma\cdot \Delta U}=\frac{\sqrt{3}\cdot 30,4\ A\cdot 14\ m\cdot 1}{56\ \frac{m}{\Omega\cdot mm^2}\cdot12\ V}=1,1\ mm^2\)
Antw: Der Querschnitt der Leitung muß \(1,5\ mm^2\) betragen.
Aufgabe 9
Vergleiche das Ergebnis aus Aufgabe 7 dieses Lernauftrages mit dem Ergebnis aus Aufgabe 7 des vorherigen Lernauftrages und begründe ob der Spannungsfall eingehalten ist oder nicht.
Die Betrachtung des Spannungsfalls fordert einen Querschnitt von \(1,5\ mm^2\), die Betrachtung der Strombelastbarkeit erfordert einen Querschnitt von \(4\ mm^2\).
Wird der Querschnitt von \(4\ mm^2\) gewählt, so ist der Spannungsfall mit eingehalten.
Hier geht es zum nächsten Lernauftrag.