Lernauftrag 13: Normalformen
Hier findest du die Aufgaben ohne Lösungen.
Bei einfachen Wertetabelle fällt es oft noch leicht eine logische Grundfunktion zu finden, welche die Wertetabelle beschreibt. Sobald mehr als 2 Eingänge verwendet werden, benötigt es viel Kreativität, um ohne weitere Hilfsmittel, zu einer Funktionsgleichung und einem Schaltbild zu gelangen.
Im Folgenden werden zwei Möglichkeiten vorgestellt, wie man aus einer Wertetabelle zu einer Funktionsgleichung gelangen kann.
Wir betrachten zum Verdeutlichen der beiden Algorithmen folgende Wertetabelle als Beispiel
| b | a | x |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Disjunktive Normalform (DNF)
Zuerst sei der Algorithmus beschrieben, mit welchem die Normalform gebildet wird.
- In allen Zeilen mit \(x=1\) werden die Eingangsvariablen mit UND verknüpft.
- Ist eine Eingangsvariable 0, so wird diese negiert.
- Alle so entstandenen UND-Verknüpfungen werden mit ODER verbunden.
Gehen wir dies am Beispiel durch:
- Zeile 2 und 4 müssen betrachtet werden. Zeile 4 ergibt: \((a\land b)\)
- Zeile 2 enthält \(b=0\), es muss somit negiert werden und ergibt: \((a\land\overline b)\)
- \(x=(a\land\overline b)\lor(a\land b)\)
Konjunktive Normalform (KNF)
- In allen Zeilen mit \(x=0\) werden die Eingangsvariablen mit ODER verknüpft.
- Ist eine Eingangsvariable 1, so wird diese negiert.
- Alle so entstandenen ODER-Verknüpfungen werden mit UND verbunden.
Gehen wir dies am Beispiel durch:
- Zeile 1 und 3 müssen betrachtet werden. Zeile 1 ergibt: \((a\lor b)\)
- Zeile 3 enthält \(b=1\). Es muss somit negiert werden und ergibt \((a\lor\overline b)\)
- \(x=(a\lor b)\land(a\lor\overline b)\)
Aufgabe 1
| c | b | a | x |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 0 |
Erstelle zu der gegebenen Wertetabelle die
- konjunktive Normalform (KNF)
- disjunktive Normalform (DNF)
DNF:
\(x=(a\land \overline b\land\overline c)\lor(\overline a\land b\land\overline c)\lor(\overline a\land\overline b\land c)\)
KNF:
\(x=(a\lor b\lor c)\land(\overline a\lor\overline b\lor c)\land(\overline a\lor b\lor\overline c)\land(a\lor\overline b\lor \overline c)\land(\overline a\lor\overline b\lor\overline c)\)
Aufgabe 2
Zeichne die Schaltnetze der beiden Normalformen aus Aufgabe 1.
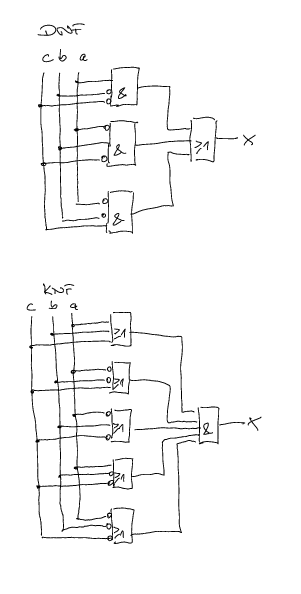
Aufgabe 3
| c | b | a | x |
|---|---|---|---|
| 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
Überlege zuerst, ob du mit der DNF oder KNF mehr Arbeit haben wirst. Wenn du unschlüssig bist, dann bilde beide Normalformen und vergleiche die Ergebnisse. Bist du dir sicher, dann bilde die kürzere Normalform und zeichne das Schaltnetz.
Überlegung:
Weniger Nullen bei x \(\rightarrow\) KNF
KNF:
\(x=(\overline a\lor \overline b\lor c)\land(a\lor b\lor\overline c)\land(\overline a\lor b\lor\overline c)\)
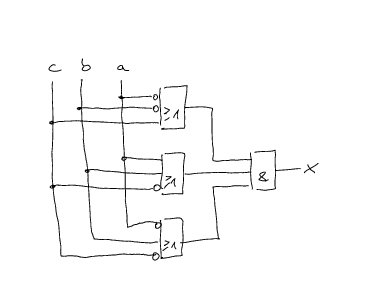
Weiter zur nächsten Lernaufgabe